- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Confused by JMPs power analysis for DOE - how do I incorporate my yield improvem...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Confused by JMPs power analysis for DOE - how do I incorporate my yield improvement goal (signal) & known current standard deviation (noise)?
I have a 7 factor DOE where my response is product yield.
I want to detect at least an 7% increase in yield above the current process average, and I know my current standard deviation for yield is +/-5% roughly. How do I incorporate these signal & noise values (signal/noise ratio) into the JMP DOE power analysis to ensure my design has enough power to detect my desired response increase?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confused by JMPs power analysis for DOE - how do I incorporate my yield improvement goal (signal) & known current standard deviation (noise)?
Hi @mjz5448,
I think the JMP Help page related to Power Analysis may help you.
If your DoE response is Yield (expressed in %), then I would complete the Power analysis with the following informations :
- Significance level : To be adjusted accordingly to your study, objectives, research stage, ...
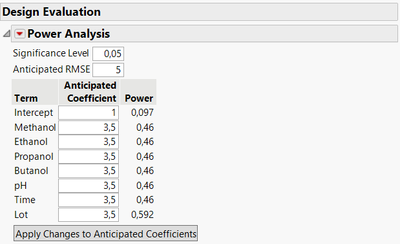
- Anticipated RMSE : Noted at 5 (or 0,05 depending on you write percentage, like maximum at 100% or at 1).
- Anticipated coefficient : Since you want to detect at least 7% increase/decrease of the response due to the factors change, I understand that between the low and high levels of each factor, Y could increase to 7% (or more). So the anticipated coefficient would be 3,5 for all your factors in this situation (since the anticipated coefficient represent the change in the response between mid and high or low levels of the factor). Don't forget to click on "Apply Changes to Anticipated Coefficients" once you have written the values so that the calculations of power can be updated.
If yes, here is what the power analysis results would look like on the dataset "Extraction2 Data" with these infos :
You might also find some useful discussions and tips in the following posts :
Should I consider power analysis in DOE?
How to get RMSE of the Power analysis for DOE
Hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confused by JMPs power analysis for DOE - how do I incorporate my yield improvement goal (signal) & known current standard deviation (noise)?
Anticipated RMSE is an estimate of the square root of the error variation, so it has same unit as standard deviation.
The formula are similar, except that for standard deviation you compare the measurements to the average, and for RMSE you compare the predicted values to the measured values.
Yes, see the conversation Should I consider power analysis in DOE? and the response from Phil to have more explanations about size of the signal and calculated power, and anticipated RMSE interpretation.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confused by JMPs power analysis for DOE - how do I incorporate my yield improvement goal (signal) & known current standard deviation (noise)?
Hi @mjz5448,
I think the JMP Help page related to Power Analysis may help you.
If your DoE response is Yield (expressed in %), then I would complete the Power analysis with the following informations :
- Significance level : To be adjusted accordingly to your study, objectives, research stage, ...
- Anticipated RMSE : Noted at 5 (or 0,05 depending on you write percentage, like maximum at 100% or at 1).
- Anticipated coefficient : Since you want to detect at least 7% increase/decrease of the response due to the factors change, I understand that between the low and high levels of each factor, Y could increase to 7% (or more). So the anticipated coefficient would be 3,5 for all your factors in this situation (since the anticipated coefficient represent the change in the response between mid and high or low levels of the factor). Don't forget to click on "Apply Changes to Anticipated Coefficients" once you have written the values so that the calculations of power can be updated.
If yes, here is what the power analysis results would look like on the dataset "Extraction2 Data" with these infos :
You might also find some useful discussions and tips in the following posts :
Should I consider power analysis in DOE?
How to get RMSE of the Power analysis for DOE
Hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confused by JMPs power analysis for DOE - how do I incorporate my yield improvement goal (signal) & known current standard deviation (noise)?
Thank you Victor.
So is RMSE essentially equivalent to standard deviation in JMP?
If I left the JMP default values of 1 for RMSE, & 1 for all coefficients, is that essentially giving me the power to detect Signal =2 = (1 + 1) for each coefficient value (aka each factor), over noise = 1 = RMSE = 1 standard deviation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confused by JMPs power analysis for DOE - how do I incorporate my yield improvement goal (signal) & known current standard deviation (noise)?
Anticipated RMSE is an estimate of the square root of the error variation, so it has same unit as standard deviation.
The formula are similar, except that for standard deviation you compare the measurements to the average, and for RMSE you compare the predicted values to the measured values.
Yes, see the conversation Should I consider power analysis in DOE? and the response from Phil to have more explanations about size of the signal and calculated power, and anticipated RMSE interpretation.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us