Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Options
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Cauchy distribution. Where is Process capability button?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
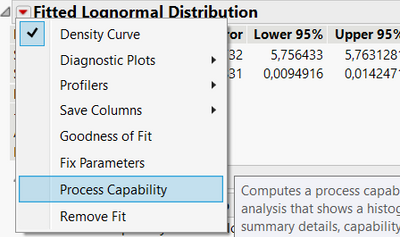
Cauchy distribution. Where is Process capability button?
Created:
Aug 12, 2020 07:45 AM
| Last Modified: Jun 10, 2023 4:17 PM
(6313 views)
Why where is no Process Capability button? Or you can't do it with Cauchy's distribution data.
1 ACCEPTED SOLUTION
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
According to the JMP Documentation, the Cauchy distribution has an undefined Mean and Standard Deviation. Based upon that, I assume JMP does not have Cp and Cpk for that distribution and thus no need for the button.
Jim
10 REPLIES 10
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
Sorry... Why is there no process capability button?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
According to the JMP Documentation, the Cauchy distribution has an undefined Mean and Standard Deviation. Based upon that, I assume JMP does not have Cp and Cpk for that distribution and thus no need for the button.
Jim
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
Yes, but then how do I calculate PPK? Should I take the nearest distribution, if it is? Or should I calculate PPK using Standard Deviation? I need to evaluate the process with nonnormal data distribution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
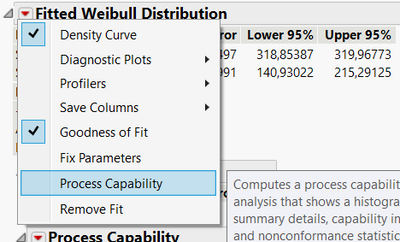
Have you tried fitting all the Distributions, and then determine which have a significant Goodness Of Fit? You could then use that distribution for your Cp and Cpk
Jim
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
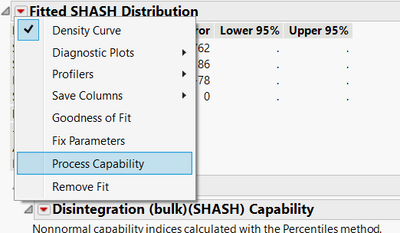
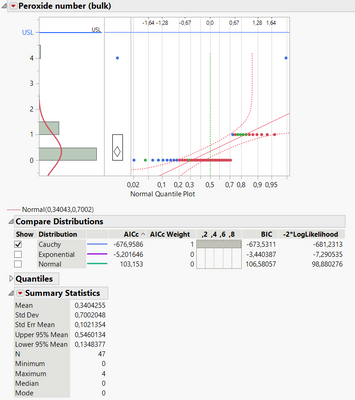
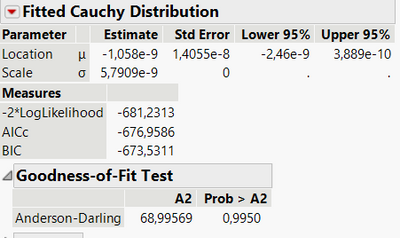
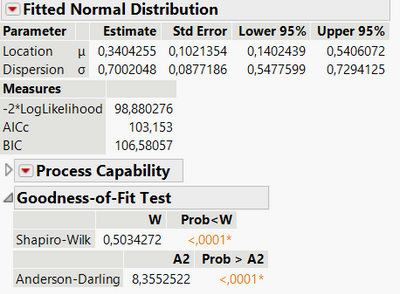
yes I click Fit all
And recieve only three, where Cauchy has a priority.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
Check out the other fits.....they might give you good estimates
Jim
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
but goodness of fit points to Cauchy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
Actually, the mean of the Cauchy distribution is defined but not the higher moments. So, no variance, no standard deviation. No standard deviation, no Ppk.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Cauchy distribution. Where is Process capability button?
And, just as an aside, if you're responsible for improving a process that outputs data that are really Cauchy distributed, you might want to update your resume...
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us