- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Capability from a bivariate regression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Capability from a bivariate regression
Hi
I read this post by Phil Kay, and it helped we some of the way towards my goal:
https://community.jmp.com/t5/Discussions/Tolerance-Interval-for-Regression/m-p/302845
Would it also be possible to calculate an expected capability from a bivariate regression, if I have a lower and upper spec limit?
Example: I have data measured for and Response(Y) at several different temperature levels (X) and I want to predict what the capability of the response is at a higher temperature.
Thanks :)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Capability from a bivariate regression
I was just sitting here, looking at the numbers, and maybe I have an idea. What if:
- I use the regression line to calculate the Response(Y) at the higher temperature (let's say 60degC): Y(60)
- I "transform" my spec limits to a set of spec limits for the residuals: Ymin - Y(60) and Ymax - Y60)
- Now, I can calculate the capability with the "residual spec limits"
Or, something completely different? :)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Capability from a bivariate regression
Here's what I suggest: Recreate the model in the Fit Model Standard Least Squares platform, then use the simulation capability within the Prediction Profiler to simulate the response for assumed variances of the x values. From there lots of options to export the simulated predictions to the Capability platforms in JMP for additional analysis and visualizations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Capability from a bivariate regression
Hi P_Bartell
Thank you for the suggestion. In my case, I want to fix the x value (at an extrapolated point) and estimate the mean and variance at this point, and thus the capability. So I am not sure you suggestion would serve the purpose, as I want to see the variation in the other dimension than you suggested. Or?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Capability from a bivariate regression
The simulator allows you to set any independent variable at any mean and estimated variance. So even if your x set point is extrapolated from your empirical space...the simulator will still work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Capability from a bivariate regression
I still think that it's not what I am looking for. Allow me to elaborate
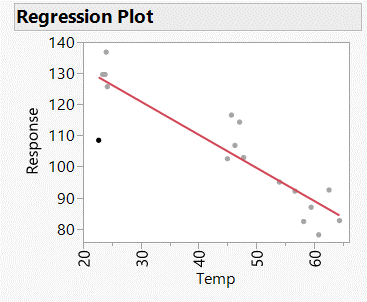
I can fit a model to my Response as a function of the temperature:
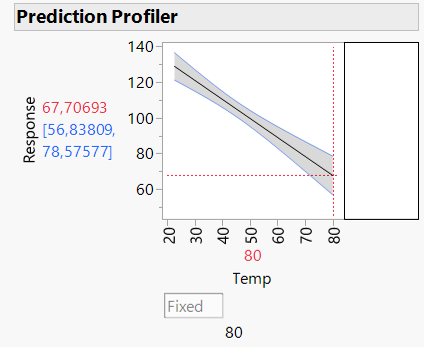
But I would like to calculate: If I fix the temperature to 80 degrees, what will the distribution of the response be?
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us