- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- CPK / PPK
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
CPK / PPK
Dear Community,
I have a "simple" question... but it put me in trouble in this moment.
For my analsys I use JMP 14.
A lot of times I need to calculate CPK and PPK.
When I ask to JMP to calculare the CPK, the software generate this analsys and give me the number.
I checked it and in this CPK number the sigma used for the calculation is "sum of square method" and not R/D2.
So... this rappresent the PPK and not the CPK...
Is it correct?
This create me some confusion in the interpretaion of the process capability.
Do you have some comment or suggestions?
Thanks in advance?
Best Reagrds,
Simone
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
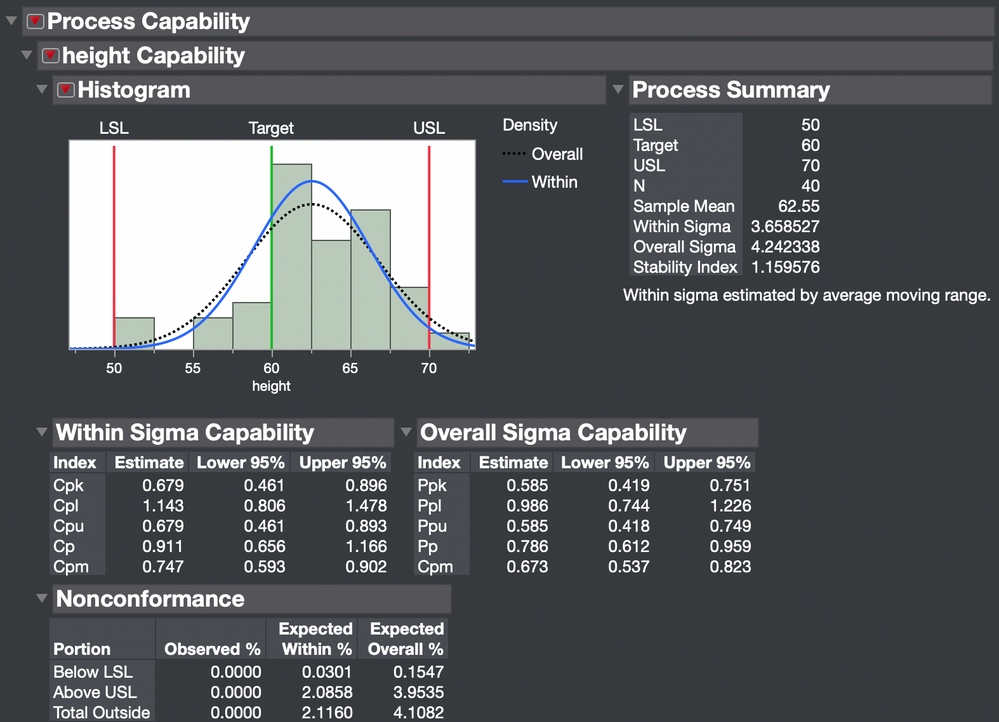
I do not have JMP 14 installed on this computer. I am using JMP Pro 15.1 to illustrate how JMP computes the indices.
You can see in this example that JMP uses the short-term estimate of sigma based on the moving range for the capability indices and the long-term estimate of sigma based on the sample standard deviation for the performance indices. I used the Process Capability command in the Distribution platform menu. How are you getting these indices?
Note to @statman that JMP recognizes the uncertainty in the estimate from a sample and provides interval estimates along with the point estimates.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
@Simone1 : In addition to the contributions from @Mark_Bailey and @statman I recommend reading thoroughly the JMP Documentation on the topic of Capability Indices. There might be some minor differences between JMP 14, which you are using, and the JMP 15 documentation linked below. Nevertheless, all options, formulas, etc. in the extensive narratives are explained there:
https://www.jmp.com/support/help/en/15.1/#page/jmp/process-capability-2.shtml#
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
Hello,
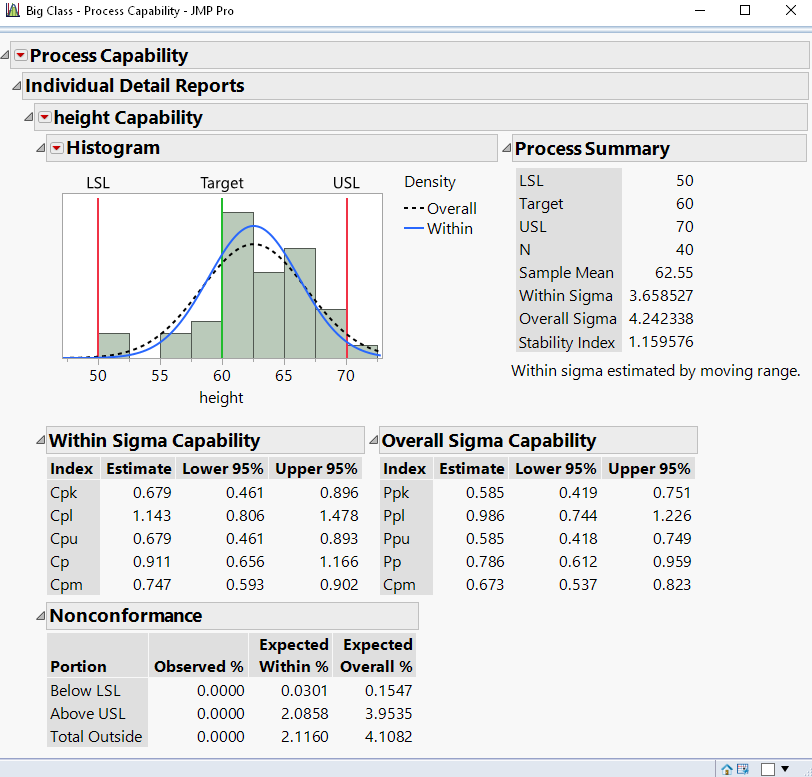
I just wanted to mention that you can get the same report that Mark is showing in his post in JMP 14 by using the Process Capability platform instead of the Distribution platform. (The Distribution capability report was updated in JMP 15.)
open("$SAMPLE_DATA\Big Class.jmp");
Process Capability(
Process Variables( :height ),
Spec Limits( :height( LSL( 50 ), Target( 60 ), USL( 70 ) ) ),
Individual Detail Reports( 1 ),
Capability Box Plots( 0 ),
Goal Plot( 0 ),
Capability Index Plot( 0 ),
Process Performance Plot( 0 )
);
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
Simone, You may not like my answer, but any of those capability ratios are a bit unrealistic. First, you must estimate 2 sample statistics (mean and standard deviation). How do you estimate these? It is based on your sample. How did you get your sample? How representative of the entire population is your sample? These are difficult questions. Usually there is some decision to sample, ...let's say 30 (I have no idea how someone came up with this number and somehow it is used universally). The variation in the sample you obtain is a function of the variables that are changing during your sampling. If variables change over and above what you have captured in your sample (or there are variables that change that are not included in your sample), then those samples are not very representative of the true variation. I'm obviously not a fan of any of those metrics (capability ratios). They are stated as one number, when we know that can't be true. I have looked at many data sets when the reported Cpk is 2, which sounds good. But when you apply simple confidence intervals around each statistic in the Cpk (mean and standard deviation) that 2.0 can go from 0.2 to 6.0. Not very useful.
There are several ways to estimate the variability in your sample. I do like R-bar/d2 as it require first a look at the data for stability (R-chart) before doing any estimate. There are of course other methods. I wouldn't get to hung up on which is right. Choose one and stick with it (to evaluate improvement over time). I suggest you read Victor Kanes paper "Process Capability Indices" (JQT, Vol. 18, No. 1 January 1986) for a thorough explanation of the different indices and Bert Gunter"s series on the use and Abuse of Cpk (statistics corner Quality Progress).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
I do not have JMP 14 installed on this computer. I am using JMP Pro 15.1 to illustrate how JMP computes the indices.
You can see in this example that JMP uses the short-term estimate of sigma based on the moving range for the capability indices and the long-term estimate of sigma based on the sample standard deviation for the performance indices. I used the Process Capability command in the Distribution platform menu. How are you getting these indices?
Note to @statman that JMP recognizes the uncertainty in the estimate from a sample and provides interval estimates along with the point estimates.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
Dear Statman, Mark and P_Bartell,
thank you for all of you feedback (appreciated).
I took hints of knowledge.
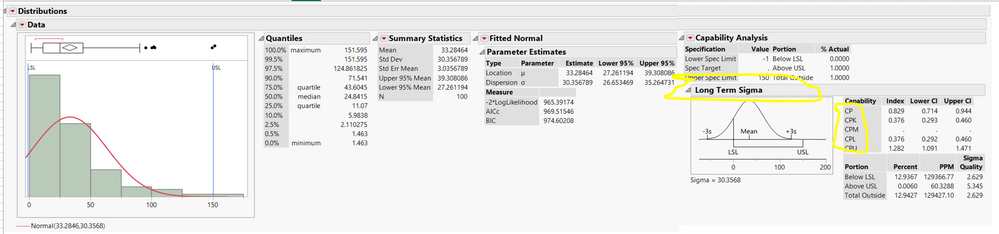
The "misleading" JMP output for me was when I apply: analyze -> distribution -> cabability analysis.
In this case, the JMP (14) output is like below (plese take in consideration that this is a full invented data, the target was not use the correct distribution... but only uderstand how CPK in JMP is calculated).
If I read this output: the CKP is calculated by the using of "overall sigma" and so this is not CPK but PPK...
This generated in me... some confusion.
I read your comment and I understand that for the capability analisys is better to use the command: analyze -> quality and process -> process capability.
Thanks.
Best regards,
Simone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
That is the capability analysis based on long term sigma that you are looking at. In this instance, the overall standard deviation is used for sigma. To use Rbar/d2(n), you need to check the box for Moving Range, Range Span in the Capability Analysis dialog when you launch capability from Distribution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
Thank you Tonya for the feedback.
I understand and this confirm my "perception" on this.
The point that confused me... was that in the JMP output... it was wtritten: "CPK".
But now all is clear.
Thanks.
Have you a good day.
Best Regards,
Simone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
I know this is an old post but I came across it recently and, if I understand your post correctly, yes I would agree that it is a bit confusing that they are using the overall sigma to calculate a "long term CPK". Long Term CPK isn't a thing in my mind. Short Term/within sigma/CPK is a thing, and long term/overall sigma/PPK is a thing. Long term/Overall Sigma/CPK is just confusing to me.
I'm guessing this is just a limitation of this specific platform that it isn't providing a seperate PPK and is saying Long-Term CPK as a synonym for it. I don't know that I've ever seen it done that way, but my experience isn't universal.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
@Simone1 : In addition to the contributions from @Mark_Bailey and @statman I recommend reading thoroughly the JMP Documentation on the topic of Capability Indices. There might be some minor differences between JMP 14, which you are using, and the JMP 15 documentation linked below. Nevertheless, all options, formulas, etc. in the extensive narratives are explained there:
https://www.jmp.com/support/help/en/15.1/#page/jmp/process-capability-2.shtml#
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CPK / PPK
Dear P_Bartell,
thanks for the technical reference on this topics.
For sure I will read it.
Best Regards,
Simone
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us