Randal Munroe publishes one of my all time favorite comics, xkcd. Last week's comic was on curve fitting, and was, arguably kind of hilarious. @Randal Munroe, dude you're hilarious. Anyone who was a discovery and heard about his Thing Explainer concept would surely agree.
So anyway, I read the comic and then dove into the data. There is an amazing tool that @brady_brady originally published for generating Homerian distributions that can be found buried in this tremendous add-in (which is a collection of other useful scripts and add-ins, a must-have). With the "Get Data Points By Clicking On Image" tool I extracted the exact data from the comic (data attached below) and then started fitting all kinds of conventional and less conventional models and some possibly dishonest models with no regard for how badly overfit the models were (even though I could/should have, with JMP Pro.)
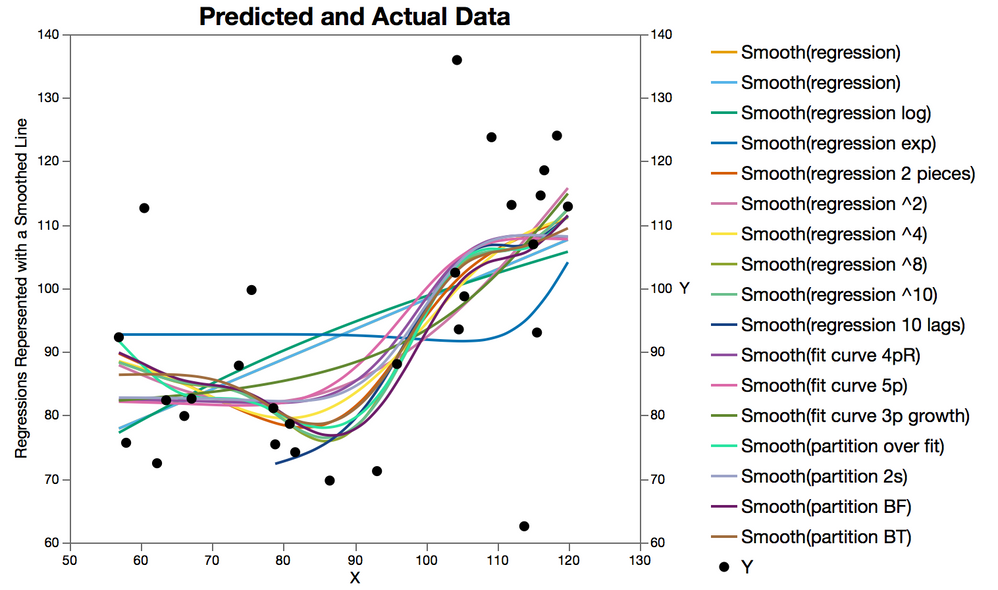
Quick Note on Axis Scale. This one seemed good to me, although it was
missing on the original figure. I could have done that too, but they there
would have been a lot of clicking and I just didn't have it in me today.
Here is a ranked table of fits
Measures of Fit for Y sorted by RSquare
|
Predictor
|
Creator
|
|
RSquare
|
RASE
|
AAE
|
notes
|
|
regression 10 lags
|
Fit Least Squares
|
|
0.9808
|
2.9103
|
2.3275
|
not legal, fit X along with a series of 10 sequential lags to the data. Works great when there is any hint of a trend in the data, might over fit, but only just a little, plus there are 11 parameter and I didn't bother to report adjusted r-square here.
|
|
partition BF
|
Bootstrap Forest
|
|
0.8469
|
7.4494
|
5.4207
|
500 trees, and some of them fell in the right direction
|
|
partition BT
|
Boosted Tree
|
|
0.6737
|
10.876
|
8.1600
|
50 layers, used defaults, un-tuned
|
|
partition over fit
|
Partition
|
|
0.6607
|
11.091
|
8.3713
|
made the minimum split size small and split to the end
|
|
regression ^10
|
Fit Least Squares
|
|
0.5687
|
12.505
|
9.3912
|
10th order polynomial, kind of wiggly
|
|
regression ^8
|
Fit Least Squares
|
|
0.5479
|
12.803
|
9.6483
|
8th order polynomial, not quite as wiggly as 10th order
|
|
regression 2 pieces
|
Fit Least Squares
|
|
0.4459
|
14.173
|
9.8317
|
used partition to split the data in two and fit two regression models
|
|
fit curve 4pR
|
Fit Curve Logistic 4P Rodbard
|
|
0.4277
|
14.404
|
10.496
|
4 parameter logistic regression, Robard model
|
|
partition 2s
|
Partition
|
|
0.4249
|
14.439
|
10.745
|
partition with only one split, results in two levels, not likely over fitted.
|
|
fit curve 5p
|
Fit Curve Logistic 5P
|
|
0.4104
|
14.620
|
10.826
|
5 parameter logistic regression
|
|
regression ^4
|
Fit Least Squares
|
|
0.3932
|
14.832
|
10.402
|
4th order polynomial
|
|
regression ^2
|
Fit Least Squares
|
|
0.3682
|
15.134
|
10.541
|
regular old 2nd order polynomial
|
|
fit curve 3p growth
|
Fit Curve Mechanistic Growth
|
|
0.3393
|
15.477
|
11.080
|
fancy non-linear model
|
|
regression
|
Fit Least Squares
|
|
0.2779
|
16.180
|
12.209
|
straight line
|
|
regression log
|
Fit Least Squares
|
|
0.2472
|
16.520
|
12.695
|
X is log transformed
|
|
regression exp
|
Fit Least Squares
|
|
0.0691
|
18.371
|
15.429
|
X is exponentiated (exp transform)
|
You might expect to find some rationale behind why I tried each of the different models but at the end of the day this is a blog not an academic paper, so don't burn too much time looking for that. I got this table from the Model comparison tool in JMP Pro, all I had to do was find all the methods and then save the prediction formula, the fancy platform did all the math.
Just in case you wanted to play with the data (and seriously, I do mean play), it should be attached below this article.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.