- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Wasatch Front JMP Users Group Discussions
Open to all JMP users in Salt Lake City, UT area- JMP User Community
- :
- JMP Users Groups
- :
- JMP Users Groups in North America
- :
- Wasatch Front JMP Users Group
- :
- Discussions
- :
- Exploring data janitorial tools in JMP and JSL
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Exploring data janitorial tools in JMP and JSL
Perfect data sets are rare. Even more so if they are manually entered! Fortunately, JMP offers data janitorial tools to help clean up our messes. The examples below demonstrate some (but definitely not all!) methods of finding and fixing two common manual entry goof ups.
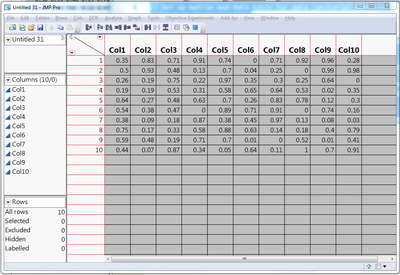
First let’s set up a quick data set to work with. You will need to copy the script below into a new script window and click the run script icon. Imagine these data are manually entered magnetic measurements of coating thickness (mm) from 10 set locations along 10 powder coated steel bars. Thickness is always less than 1 due to process controls. It is possible to have a bare uncoated spots of thickness 0.
// Set up matrix and data table for data janitorial exercise
Names Default To Here(1);
// Load random matrix with simulated data collection errors
rndMat = [
0.35 830 0.71 0.91 0.74 . 0.71 0.92 0.96 0.28,
0.50 0.93 0.48 0.13 0.70 0.04 0.25 . 0.99 0.98,
0.26 0.19 750 0.22 0.97 0.35 0.30 0.25 0.64 .,
0.19 0.19 0.53 0.31 0.58 0.65 0.64 0.53 0.02 0.35,
640 0.27 0.48 0.63 0.70 0.26 0.83 0.78 0.12 0.30,
0.54 0.38 0.47 . 0.89 0.71 0.91 . 0.74 0.16,
0.38 0.09 0.18 0.87 0.38 0.45 0.97 0.13 0.08 0.03,
0.75 0.17 0.33 580 0.88 0.63 0.14 0.18 0.40 0.79,
0.59 0.48 0.19 0.71 0.70 0.01 . 0.52 0.01 0.41,
0.44 0.07 0.87 0.34 0.05 0.64 0.11 1.00 0.70 0.91
];
// Make data table from random matrix
dtNew = As Table( rndMat );
Now let’s look for errors by plotting and summarizing our data. I am focusing on data cleaning in this example but in real life I am also gaining some basic understanding of my data. Remember, before any analysis PDD (plot the data dummy)!!
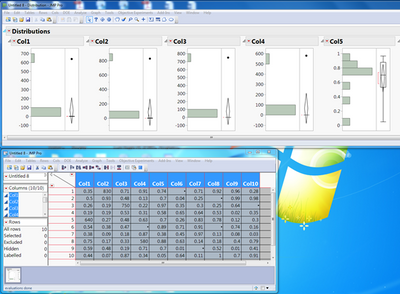
The distribution platform is a great tool for seeing abnormalities in data. Notice there are entries 1000 times greater than expected in our data set. I personally encounter data where inspectors/operators miss the decimal or even choose to omit all decimal places to be faster! It is a good idea to verify errors like this with the operators before making changes.
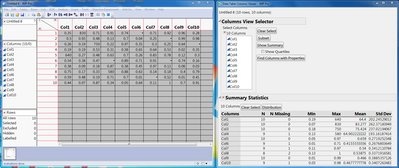
The Columns Viewer is quick and easy summary tool. The image below shows a summary table for all columns. Notice there are 10 missing values in our data. Missing values where zeros should be is a very common manual entry error, even more common than misplaced or dropped decimals in my experience. This may seem trivial with our small table where we can easily see all of the missing values. But, imagine the difficulty if our data set has thousands or even millions of rows of data! Haystacks and needles come to mind.
Summary statistics can be used in the same way we used the distribution platform above. Notice max values for col1-col4 are 100 times greater than expected –same as we learned in distribution.
Our exploratory analysis has identified 2 types of errors in our data. Missing decimals and missing values that should be zeros. Now let’s fix them! In a small table like ours it is pretty easy to make the necessary changes manually in the data table. We are going to assume that this is not the case and that more efficient methods are needed.
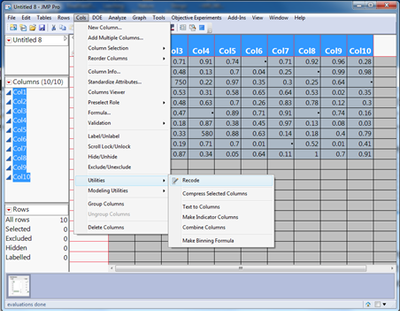
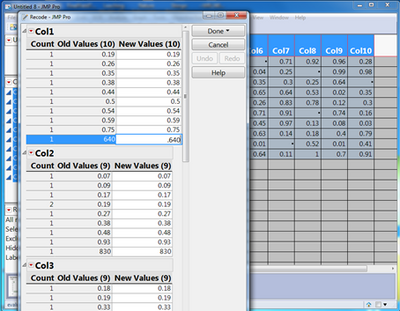
The Recode Utility in JMP provides a menu driven option for changing values in a data table. Columns must be selected in order to access the utility. Both of our errors can be fixed in recode.
Now imagine our data set has 10000 rows and 100 columns. All of a sudden, recode is not as attractive. Fortunately for us JSL (JMP scripting language) can be used to solve our problem quickly and efficiently!
First let’s find and fix all of our data with missing decimals. It is easy to imagine automating a manual find and fix routine with loops. As you will see this does get the job done.
To keep this exercise simple and clear, close the data table and script window. Past the script below into a new script window and run the script.
Names Default To Here(1);
// Load random matrix with simulated data collection errors
rndMat = [
0.35 830 0.71 0.91 0.74 . 0.71 0.92 0.96 0.28,
0.50 0.93 0.48 0.13 0.70 0.04 0.25 . 0.99 0.98,
0.26 0.19 750 0.22 0.97 0.35 0.30 0.25 0.64 .,
0.19 0.19 0.53 0.31 0.58 0.65 0.64 0.53 0.02 0.35,
640 0.27 0.48 0.63 0.70 0.26 0.83 0.78 0.12 0.30,
0.54 0.38 0.47 . 0.89 0.71 0.91 . 0.74 0.16,
0.38 0.09 0.18 0.87 0.38 0.45 0.97 0.13 0.08 0.03,
0.75 0.17 0.33 580 0.88 0.63 0.14 0.18 0.40 0.79,
0.59 0.48 0.19 0.71 0.70 0.01 . 0.52 0.01 0.41,
0.44 0.07 0.87 0.34 0.05 0.64 0.11 1.00 0.70 0.91
];
// Make data table from random matrix
dtNew = As Table( rndMat );
myCols = N Cols( dtNew );
For( q = 1, q <= myCols, q++,
col = Column(q);
For Each Row( col[] =
If(
col[] > 100, col[]/1000, col[]
);
If(
Is Missing(col[])==1, col[] = 0, col[]
);
);
);
The dropped decimal places and missing zeros are now fixed! This method is legit but lengthy and may be slow with larger data sets. In my opinion logical indexing is a better way to go. In JSL logical indexing is accomplished using the Loc() function. This will be a bit easier to show than to tell.
Close the table and script window (save if you want). Paste the following script to a new script window. Click run script.
Names Default To Here(1);
// Load random matrix with simulated data collection errors
rndMat = [
0.35 830 0.71 0.91 0.74 . 0.71 0.92 0.96 0.28,
0.50 0.93 0.48 0.13 0.70 0.04 0.25 . 0.99 0.98,
0.26 0.19 750 0.22 0.97 0.35 0.30 0.25 0.64 .,
0.19 0.19 0.53 0.31 0.58 0.65 0.64 0.53 0.02 0.35,
640 0.27 0.48 0.63 0.70 0.26 0.83 0.78 0.12 0.30,
0.54 0.38 0.47 . 0.89 0.71 0.91 . 0.74 0.16,
0.38 0.09 0.18 0.87 0.38 0.45 0.97 0.13 0.08 0.03,
0.75 0.17 0.33 580 0.88 0.63 0.14 0.18 0.40 0.79,
0.59 0.48 0.19 0.71 0.70 0.01 . 0.52 0.01 0.41,
0.44 0.07 0.87 0.34 0.05 0.64 0.11 1.00 0.70 0.91
];
// Find location of errors and replace with correct values
rndMat[Loc(rndMat>100)] = rndMat[Loc(rndMat>100)]:\1000;
rndMat[Loc(IsMissing(rndMat))] = 0;
dtNew = As Table( rndMat );
Take a look at the results! We fixed both the missing decimal and missing zeros with 2 lines of code and no loops! Take note that to avoid loops I generated a new data table with correct values. If you want to keep an existing table then a loop is needed to assign values to each column in the data table. I will let you all experiment with this on your own.
This is what happened. Loc(rndMat>100) is a matrix of indices in rndMat where values are greater than 100. rndMat[Loc(rndMat>100)] = rndMat[Loc(rndMat>100)]:\1000 replaces the values at these indices with the current value divided by 1000. Replacing missing values is simpler as we are just replacing missing values with zero.
More information on the Loc() function can be found in Chapter 7 of the scripting guide. The scripting guide can be found under Help_Books. Logical indexing has utility beyond data cleaning and is worthy of study if new to you.
Hope this has exercise helps you all unlock more of the power of JMP.
Enjoy!
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us