When I was first learning design of experiments in graduate school, we covered the usual suspects: factorial and fractional factorial designs with two-level factors. These designs are popular precisely because they allow for main effects to be independent of one another; the focus of fractional factorials being to save on runs at the expense of aliasing with interaction effects. While learning about resolution and how to choose one fractional factorial over another, I had come to accept that the number of runs was always going to be some power of 2. When we briefly touched on Plackett-Burman designs, I saw that the run size could be generalized to a multiple of 4. But beyond that, it seemed like a good design wasn’t possible.
Flash forward several years and I’m playing around with the Custom Design platform in JMP for generating experimental designs for clients at Sandia Labs. That was the first time I’d seen where you could specify any run size you liked. Now I tended to stick with run sizes that were, preferably, multiples of the factor level combinations as it just felt right. But it was around that time that a question started to nag me; was it possible to create an optimal design for any run size?
Now, to clarify, the answer is technically yes as JMP, much like other software, uses an algorithm to search for the optimal design given a starting one. But that’s not exactly what I was asking. What I wanted to know was if it was possible to directly construct one, much like the factorial and fractional factorial designs.
For those unaware, factorial and fractional factorial designs are essentially special types of matrices known as Hadamard matrices. What makes these matrices special is that, when you take the transpose of the matrix and multiply it by the original matrix (e.g., X^t*X), you end up with a diagonal matrix. This is precisely why they are used as factorial and fractional factorial designs; the diagonal matrix is equivalent to the covariance matrix and so represents independent main effects.
When I learned this fact, it made me want to explore my question even more. But it wasn’t until my first year at JMP that I was able to do so. I started as I usually do; playing around with the mathematics, slowly gaining insight into possible construction methods. I discussed my work with my colleagues, @Ryan_Lekivetz and @joseph_morgan, and Ryan sent me an article by Dennis Lin on supersaturated designs that he thought might pique my interest due to some similar themes. While it didn’t directly relate to my work, one of the references did. And it’s there that everything changed.
The Joy of Rediscovery
It felt like I had stumbled upon a hidden door that, upon opening it, revealed a strange and wonderful new world (the similarity to Lucy’s experience in C.S. Lewis’s The Lion, The Witch, and The Wardrobe, while unintended, is quite appropriate). Reading that reference led to another, which led to another, and on and on and on until I had compiled quite the collection of literature. What was so fascinating about these papers? They all discussed direct construction methods for generating D-optimal designs for two-level factors for virtually any run size!!
Now, to avoid hyperbole, I should say that even though such methods exist, they do not exist for every single possible run size and some of the methods are quite complex. But the fact that direct methods did exist excited me! And, as it turns out, for a good majority of practical cases, the construction procedures were quite simple and involved adding or subtracting runs from the well known factorial and fractional factorial designs (it turns out this was what my personal research was going towards; per usual, I find myself often rediscovering the wheel…oh well). In fact, I was surprised I had never heard of some of these methods during my time in graduate school. Then again, it might be something you would learn only after you’ve mastered factorial and fractional factorial designs, which require a significant time to master on their own.
I shared these methods with my colleagues, who immediately saw the impact such methods could have in creating optimal designs. Imagine that, instead of having to implement a search algorithm to hopefully find a D-optimal design, you could build one from scratch and have it mathematically guaranteed to be D-optimal. Now imagine you could do this for a wide range of run sizes; again, not all, but a vast majority that is sufficient to cover practical situations. Well guess what? You don’t have to imagine it anymore!!
The Punchline
That’s right folks. In JMP 15, we now implement the simple construction procedures for generating D-optimal designs right into the Custom Design platform! “That’s nice,” you might say, “but how does this change things?” Well, yes, it’s not as visible or glamorous as, say, creating a new supersaturated design construction platform. But perhaps the following demonstration may help illustrate:
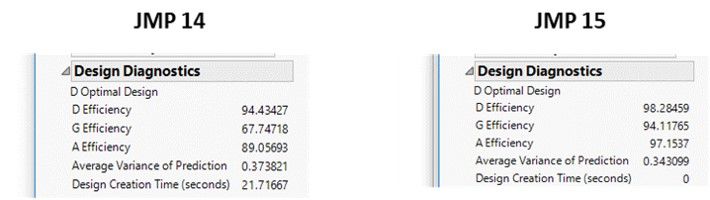
Both of these designs involve the same number of factors (31) and run sizes (34) and both were created to be D-optimal. Note that the run size is not a multiple of 4 (or you can double check for yourself, I won’t judge…just stare condescendingly). In the version on the left, it took nearly 30 seconds for the algorithm to find what it hopes is the D-optimal design. In the version on the right, it created a clearly more D-efficient design almost instantaneously. Now, at this point, I’d like to mention that I come from an accelerated testing background. I say this because, in that context, we’re used to cranking things up to extreme levels. So how about we crank up this here example to an extreme?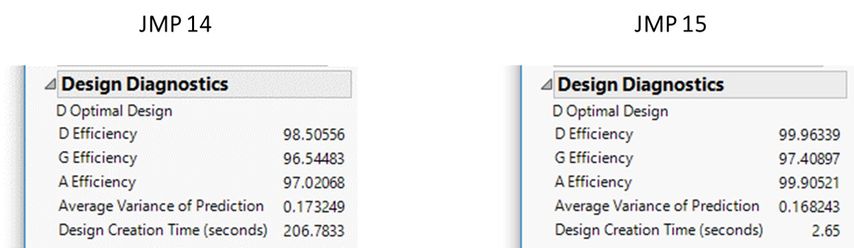
In this case, the number of factors is 531 and the number of runs is 1059 (an experimenter’s dream and worst nightmare all in one). In the version on the left, it took nearly three minutes for the algorithm to find what it hopes is the D-optimal design. For the version on the right, it took nearly 3 seconds to report the more D-efficient design. I say report instead of create because the creation step is about as long as it was for the previous example; the rest of the time is spent laying out the design and getting the diagnostics in the final report, just because it’s so massive. If that doesn’t prove to you how amazing this improvement is, I don’t know what will!!
Business as Usual
As you’ll be seeing in several upcoming blog posts, JMP 15 is brimming with new features. And if you attended the JMP Discovery Summit conference in Tucson, you no doubt got a hands-on look. While you might be bouncing off the walls with excitement (or perhaps you’re more subdued in your excitement, no judgement here), for us developers and testers it’s business as usual: making sure our customer’s statistics needs are always being met and even surprising them with what they never knew they needed. So enjoy this new version and all it has to offer and definitely make sure to let us know your feedback!!