Throughout my time at JMP, I have had many design problems that needed the use of covariates, both for my own problems and to help customers find a solution to their design problem. What I have noticed is that many customers, even very experienced ones, are not aware of the covariate option in the Custom Design platform.
To start off, I want to point out it has lived right in the Add Factor dropdown in Custom Design since JMP 10, and you may not have even noticed until now:
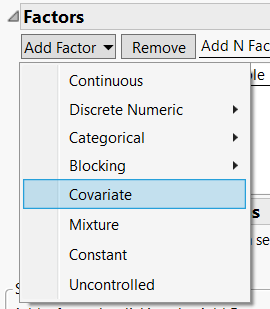
What is a covariate?
Part of the confusion stems from the use of the term covariate. In some contexts, you will see it used as an effect to control for, but not of primary interest (ANCOVA), and you may even see it loosely used for any independent factor in defining a model.
In a designed experiment, a covariate is an input variable that we want to account for in our experiment but we cannot control it to be any value in the way we can for other types of factors. However, if we can measure the values of such inputs ahead of time, we can account for them when designing the experiment.
When would I use a covariate?
If you think of a covariate from the standpoint of “uncontrolled, but observable ahead of time,” there are a few different use cases that come up. You may often hear the idea of a candidate set. In the Custom Designer, specifying the covariate factors produces a “candidate set” of runs for the Custom Designer to use. In Custom Design, the candidate set is specified from a data table. Very often, we have additional controllable factors (that can take on any value in the range), that we can allow the Custom Designer to pick as it sees fit (the way we usually define factors).
Broadly speaking, I tend to break the use of covariates into two cases:
- Using a subset of the rows.
- Using all the rows.
Using a subset of rows
When using the Custom Designer to select a subset of the covariates set, the idea is to use the values of the covariates that we can measure ahead of time to pick the best runs from the candidate set according to the experimental goal. This ends up being much more efficient than simply taking a random sample.
For an excellent example, I like to point people to Chapter 9 of Optimal Design of Experiments: A Case Study Approach. If you do not have a copy of the book, you can read an outline of the idea in an earlier blog post from Bradley Jones.
Another common use case is to provide a candidate set that enforces some constraint on the design space. While this can be done using factor constraints from the Custom Designer, the candidate set approach is useful when the region is quite complex, or if you want the runs of an experiment to have a certain structure. For example, you might want continuous variables to take on only five distinct values or restrict the number of non-zero factors in any given experimental run.
Using all the rows
Like the subset case described above, this can occur when all our experimental units are chosen, and we can measure some uncontrollable values before designing the experiment.
A common use case that may be less obvious is to force a desired structure for a subset of the factors.
For instance, say if you were designing a 12-run experiment with one two-level categorical factor, X1 with levels A and B, and four continuous factors, X2-X5, with an added restriction that for the categorical factor, 1/3 of the runs need to be at level A and 2/3 at level B.
All we need to do is create a data table for the categorical factor with 12 runs, and a column labeled with that factor name. Put four rows as A, and eight rows as B.
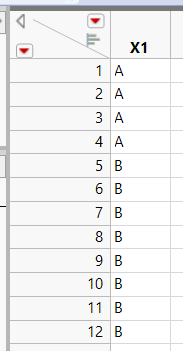
In Custom Design, choose Add Factor->Covariate, and then add the remaining four continuous factors. If we keep the number of runs at 12 before clicking Make Design, like this,

the resulting design will force the runs for X1 as specified by the candidate set (with the desired ratio) and design for the optimal settings for the continuous factors.
Other examples using this idea from previous blog posts include the creation of an experiment robust to a linear trend in the response over time or ensuring a definitive screening design structure for a subset of the factors, such as an experiment for hard-boiled eggs.
Anything else?
We have made some improvements to covariate handling in JMP 16. I've highlighted those new pieces in another post.