It’s been years since I last dyed Easter eggs, but this year we decided to give it a try. This means I’ve suddenly found the need to hard-boil some eggs. One of my favorite experiments that I’ve blogged about was the eggciting eggsperiment, so it’s the perfect time to revisit that experiment. That experiment has changed the way we hard-boil eggs at home – we’ve been using the boiling start method since.
I received a number of suggestions (and even online calculators) from the previous eggsperiment, so this time I wanted to play around more with the cooking factors involved with the pot of water. Previously, the only hard-to-change factor was if the eggs were placed into hot or cold water. We’ll investigate further this time, with hard-to-change factors:
- Cooking Start (Hot/Cold)
- Cooking Time (10 minutes, 12 minutes, 14 minutes)
- Salt (0 tsp, ½ tsp, 1 tsp)
- Vinegar (0 tbsp, ½ tbsp, 1tbsp)
Each pot will have two cups of water. For a hot cooking start, cooking time begins when the egg is placed into boiling water. For a cold cooking start, cooking time starts when the egg is removed from the heat after boiling. You can read more about cooking method in the previous eggsperiment and links within it.
I also have two easy-to-change factors:
- Egg (brown, white)
- Cooling Method (cold water/ice water)
For those of you who are interested only in the results, you’ll have to wait until next time. If you want to know how I’ve designed the experiment, read on…
The Design Setup
There are interesting considerations for this experiment. Firstly, I have three continuous factors in the hard-to-change factors that I’m interested in at three levels, along with a two-level categorical factor. I could certainly enter additional effects in the Custom Designer to accomplish the three levels for the continuous factors, but it sure would be nice if the design for the whole plot factors was a definitive screening design (DSD). Here is what a DSD would look like, if I enter those four factors in the Definitive Screening Design platform, found under DOE->Definitive Screening Design:
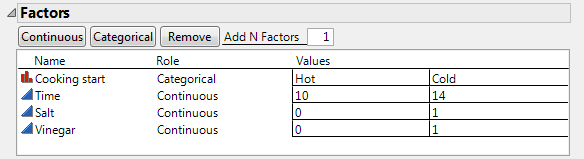
I end up with a 14-run design after choosing the “No Blocks Required” option.
But I still have the easy-to-change factors. To top it off, I only have 24 eggs, which isn’t nicely divisible by 14.
Hard-to-Change Covariates
Fortunately, in JMP 12 we added the ability to create a design with hard-to-change covariates. This means that I can have the design on the whole-plot factors be based on a DSD (although I might not have equally-sized whole plots), and it’s assigning the easy-to-change factors according to the design specifications.
Hard-to-change covariates?
With the 14-run DSD data table open, I load in the design the same way I usually do covariates. After launching Custom Design (DOE->Custom Design), under “Add Factor”, I find “Covariate.”
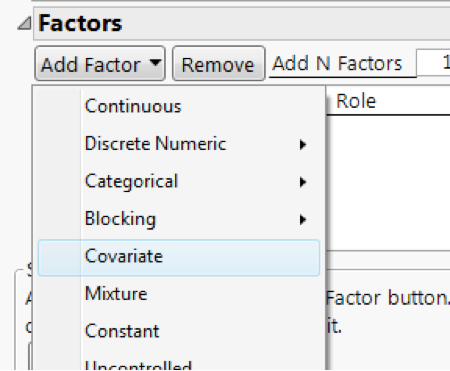
Selecting the four hard-to-change factors and clicking OK, they are loaded in as covariates, and I can now add the remaining two factors via “Add Factor”. My factors table looks like this:
Starting from JMP 12, I can change the role of the covariates by clicking on an entry under the Changes column for one of them, and choosing “Hard”. This automatically changes all the covariates to hard-to-change.
The Model
If using a DSD for the whole-plot factors, I feel comfortable that those main effects should be minimally aliased with second-order effects among the whole-plot factors. However, I now have two new factors to consider. Ideally, I get a design in which I can reduce the aliasing of second-order effects on the main effects, but also have the chance to detect a few active second-order effects. I used a model with the quadratic effects for the three continuous whole-plot factors, all the interactions involving one whole-plot and one sub-plot factor, and the interaction of the sub-plot factors. This isn’t the final model I’ll use when fitting, but should help me with model selection when it comes to analysis.
I chose alias optimality to create the design (from the red triangle menu Optimality Criterion->Make Alias Optimal Design), although I had similar results with D-optimality. This would help ensure that my main effects are minimally aliased with the second order effects, and I have a reasonable chance of detecting any large second effects that may occur.
How Many Whole Plots?
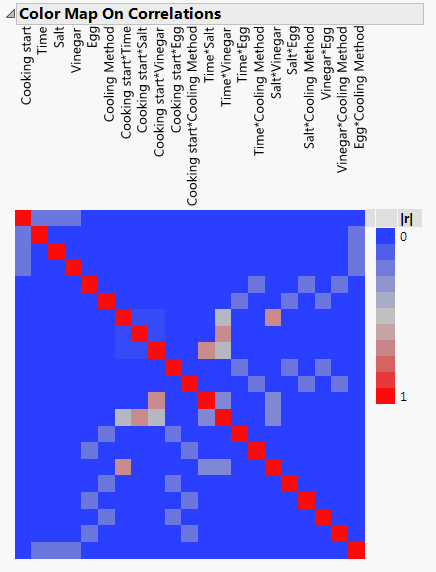
I know my overall run size is constrained to 24 runs. Using 14 whole plots is a far cry from the six I used in the first eggsperiment, but I also have more factors in the whole plots. The first design I tried used 14 whole plots (i.e., the full DSD). I was quite happy with the design, but it would be nice to reduce the pots of eggs that I need. I tried a different number of whole plots, and ultimately decided on 12. The biggest difference is a loss of power for the quadratic effects, but I’m really only expecting to detect quadratic effects if they are quite large. I also end up with two eggs per pot, which I prefer from the psychological standpoint of not having a pot of water with a single egg. Did I still maintain something that has the nice properties from a DSD? Based on the color map on correlations, it was close enough for my liking.
Next Time
Stay tuned for the results, but I’d be curious to hear how you hard-boil your eggs -- what did I miss this time? Thanks for reading!