In 2011, my colleague Prof. Chris Nachtsheim and I introduced Definitive Screening Designs (DSDs) with a paper in the Journal of Quality Technology. A year later, I wrote a JMP Blog post describing these designs using correlation cell plots. Since their introduction, DSDs have found applications in areas as diverse as paint manufacturing, biotechnology, green energy and laser etching.
When a new and exciting methodology comes along, there is a natural inclination for leading-edge investigators to try it out. When these investigators report positive results, it encourages others to give the new method a try as well.
I am a big fan of DSDs, of course, but as a co-inventor I feel a responsibility to the community of practitioners of design of experiments (DOE) to be clear about their intended use and possible misuse.
So when should I use a DSD?
As the name suggests, DSDs are screening designs. Their most appropriate use is in the earliest stages of experimentation when there are a large number of potentially important factors that may affect a response of interest and when the goal is to identify what is generally a much smaller number of highly influential factors.
Since they are screening experiments, I would use a DSD only when I have four or more factors. Moreover, if I had only four factors and wanted to use a DSD, I would create a DSD for six factors and drop the last two columns. The resulting design can fit the full quadratic model in any three of the four factors.
DSDs work best when most of the factors are continuous. That is because each continuous factor has three levels, allowing an investigator to fit a curve rather than a straight line for each continuous factor.
When is using a DSD inappropriate?
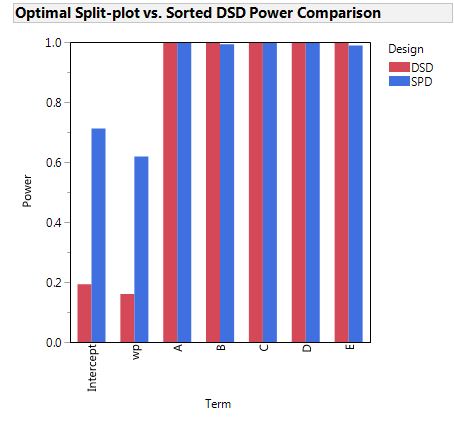
Below, the optimal split-plot design dramatically outperforms the Definitive Screening Design created by sorting the hard-to-change factor, wp. See point 4) below.
1) When there are constraints on the design region
An implicit assumption behind the use of DSDs is that it is possible to set the levels of any factor independently of the level of any other factor. This assumption is violated if a constraint on the design region makes certain factor combinations infeasible. For example, if I am cooking popcorn, I do not want to set the power at its highest setting while using a long cooking time. I know that if I do that, I will end up with a charred mess.
It might be tempting to draw the ranges of the factors inward to avoid such problems, but this practice reduces the DSD’s power to detect active effects. It is better to use the entire feasible region even if the shape of that region is not cubic or spherical.
2) When some of the factors are ingredients in a mixture
Similarly, using a DSD is inappropriate if two or more factors are ingredients in a mixture. If I raise the percentage of one ingredient, I must lower the percentage of some other ingredient, so these factors cannot vary independently by their very nature.
3) When there are categorical factors with more than two levels
DSDs can handle a few categorical factors at two levels, but if most of the factors are categorical, using a DSD is inefficient. Also, DSDs are generally an undesirable choice if categorical factors have more than two levels. A recent discussion in The Design of Experiment (DOE) LinkedIn group involved trying to modify a DSD to accommodate a three-level categorical factor. Though this is possible, it required using the Custom Design tool in JMP treating the factors of the DSD as covariate factors and adding the three-level categorical factor as the only factor having its levels chosen by the Custom Design algorithm.
4) When the DSD is run as a split-plot design
It is also improper to alter a DSD by sorting the settings of one factor so that the resulting design is a split-plot design. For the six factor DSD, the sorted factor would have only three settings. There would be five runs at the low setting, three runs at the middle setting and give runs at the high setting. Using such a design would mean that inference about the effect of the sorted factor would be statistically invalid.
5) When the a priori model of interest has higher order effects
For DSDs, cubic terms are confounded with main effects, so identifying a cubic effect is impossible.
Regular two-level fractional factorial designs and Plackett-Burman designs are also inappropriate for most of the above cases. So, they are not a viable alternative.
What is the alternative to using a DSD in the above cases?
For users of JMP, the answer is simple: Use the Custom Design tool.
The Custom Design tool in JMP can generate a design that is built to accommodate any combination of the scenarios listed above. The guiding principle behind the Custom Design tool is
“Designs should fit the problem rather than changing the problem to suit the design.”
Final Thoughts
DSDs are extremely useful designs in the scenarios for which they were created. As screening designs they have many desirable characteristics:
1) Main effects are orthogonal.
2) Main effects are orthogonal to two-factor interactions (2FIs) and quadratic effects.
3) All the quadratic effects of continuous factors are estimable.
4) No 2FI is confounded with any other 2FI or quadratic effect although they may be correlated.
5) For DSDs with 13 or more runs, it is possible to fit the full quadratic model in any three-factor subset.
6) DSDs can accommodate a few categorical factors having two levels.
7) Blocking DSDs is very flexible. If there are m factors, you can have any number of blocks between 2 and m.
8) DSDs are inexpensive to field requiring only a minimum of 2m+1 runs.
9) You can add runs to a DSD by creating a DSD with more factors than necessary and dropping the extra factors. The resulting design has all of the first seven properties above and has more power as well as the ability to identify more second-order effects.
In my opinion, the above characteristics make DSDs the best choice for any screening experiment where most of the factors are continuous.
However, I want to make it clear that using a DSD is not a panacea. In other words, a DSD is not the solution to every experimental design problem.