- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: what are the right or common steps to successfully build a structural equati...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
what are the right or common steps to successfully build a structural equation model?
I have learned theories about structural equation modeling but don't have enough experience building a structural equation model. I have spent too much time struggling with building a good SEM. I have some questions about the steps to build a structural equation model and hope someone would give me the answer and save me. I am using JMP pro 16.
Q1. Is there any problem with my own steps to build a structural equation model and is there any step I missed?
My steps:
1. I am using maximum likelihood estimation, so check the distribution of each variable that may be endogenous variable in the model and transform any of them that is not normal distritbuion;
2. rescale some variables with very large or small variance to avoid potential estimation problems;
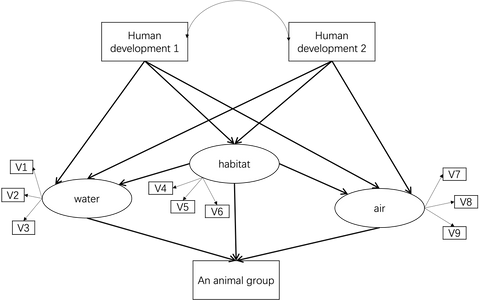
3. I have more than 50 variables related with several aspects (around 3 - 5) of a natural system (eg. water, habitat, air). I would like to use some of them to build 3 to 5 latent variables which represent different aspects of the natural system. Then I would like to use some observed variables representing human development as exogenous variables in final structural equation model to see how human development affects several aspects of a natural system then affects an animal group. The following diagram is the conceptural model.
4. run correlation analysis for the 50 variables, based on the result and existing theories, I grouped variables with correlations > 0.3 and theoretically falling into the same aspect (some variables were in several groups). So I got several groups of variables.
5. run factor analysis for each group. In each group, I selected 2-3 variables that have high and similar loadings in the same factor as indicators for a latent variable (this step tends to be subjective);
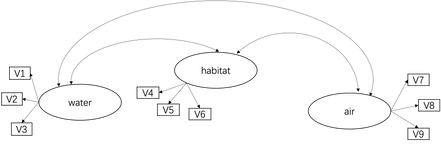
6. run confirmatory factor analysis with selected variables (see diagram below). If pass (based on fit indices, indicator reliability, composite reliability, construct maximal realiability, construct validity matrix), use these latent variables to build structural equation model with observed variables (human development, animal group). If not pass, change the combination of variables until pass.
7. build structural equation model and check the fit indices.
Q2: what are the right or common steps to successfully build a structural equation model?
I have seen some answers or videos mentioning conducting clustering analysis, PCA, and factor analysis before CFA but I am not sure. Also could anyone recommend me any articles/books/videos giving step-by-step instructions to build a SEM? Thanks.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: what are the right or common steps to successfully build a structural equation model?
Hi,
I am sorry to see that you have not received a reply yet. One reason for this is that SEM is relatively new to the community of JMP users.
I think it might also help if you could post a single question in your post. Discussion posts that are short and specific requests tend to get the best response. Posting the simplest possible example data to illustrate what you are trying to do is also a good thing in most cases.
I know a little about SEM (it was one of the modules in my Stats MSc). From what I know, I think it is hard to give a prescription for "the right way" to build a structural equation model. I don't know enough to comment on the approach that you have proposed. I would say that 50 variables is a lot more than I have seen in SEM examples, so this might be difficult.
In terms of resources, you should look for anything by Laura Castro-Schilo (@LauraCS). For example,
Also, my colleague, @jordanwalters, is posting articles about SEM every month in the JMPer Cable. Jordan might have some suggestions for resources that he found useful when learning about SEM.
Sorry I couldn't really answer your questions. But I hope this helpful.
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: what are the right or common steps to successfully build a structural equation model?
Hi lujc07,
Resources for SEM:
I highly recommend seeking out some of Laura's (@LauraCS) resources and posts as a good starter for using SEM in JMP.
A good one to watch is: https://community.jmp.com/t5/Discovery-Summit-Americas-2020/ABCs-of-Structural-Equations-Models-2020...
Additionally, there are a number of good SEM texts out there, I think a good starter is "Principles and Practice of Structural Equation Modeling" by Rex Kline, it has an applied bent to it. Other authors you'll see are Ken Bollen, Schumacker & Lomax, Rick Hoyal, and many others; all their texts are great resources as well and some will be more technical than others. Most of the texts will likely use examples from education and social science's but the approaches apply generally. The technique is simply used widely in those areas.
Re: Q2: I think it'd generally be considered most appropriate for SEM to follow Exploratory Factor Analysis (EFA / FA) as opposed to some of the other dimension reduction techniques you listed (PCA, clustering, etc.). However, if you're reading literature, you might see other ones like PCA being used prior. A useful ordering in your head for thinking about it might be Correlation Matrix -> EFA -> CFA -> SEM.
Re: Q1: Steps 1-6 are a good general set of steps for moving into SEM. In fact, I think sometimes people forget these important earlier steps and just try to build a model right away which can lead to headaches. A couple of suggestion I have:
Step 5:
run factor analysis for each group. In each group, I selected 2-3 variables that have high and similar loadings in the same factor as indicators for a latent variable (this step tends to be subjective).
In your FA step I would consider including all the variables (v1-v9 etc) associated with your latent variables "water, air, and habitat" in the FA (you possibly did this but I wasn't quite sure). The reason is, it will help you identify those variables that may cross load with these other factors and help you decide if you want to include them or not. An item may look great when it’s on its own in a small subset but when it’s included with the other variables it may not be one that you want to retain. It will also help you see if these factors are separating out as you'd expect.
Additionally, use at least 3 variables for a latent variable (good rule of thumb) and if you have more than that, that are appropriate, and load well onto a factor (such as 4 or 5) bring those along as well no need to toss them out if they measure the construct well. If you're in the position of having enough data just note it is ideal if you can do EFAs on part of the data (a test set) and then follow-up with CFAs on another set of data (a validity set). The factor structure for the EFAs is going to be driven by the data and following it up with CFAs on a new set of data will help you identify if the item parameters and factors replicate well.
Step 6:
- 6. run confirmatory factor analysis with selected variables (see diagram below). If pass (based on fit indices, indicator reliability, composite reliability, construct maximal realiability, construct validity matrix), use these latent variables to build structural equation model with observed variables (human development, animal group). If not pass, change the combination of variables until pass.
After you've settled on your variables for your latent variables (using all the information you noted in your post) and the observed variables you want to use then think about the different SEMs you want to test. The goal of SEM is to use theory or more generally your knowledge of an area to test out multiple competing models. A competing model is one that differs in its parameterization. For a simple example, if you removed the path between "Human Development 2" and "Habitat" that would result in a new, slightly simpler model that you could test (a nested model). The model differs by 1 parameter and would result in a new set of fit indices and results. If that model fits practically as well as the model that included that path we might conclude there is statistical evidence for it being a more parsimonious model that fits just as well as a more complex one. You can expand on this idea and run multiple models until you settle on your model that exhibits good fit and is reasonable for your theory. When modifying your model to try other models, I recommend being intentional with your changes to paths, and testing things that would make sense to you and the theory your interested in.
In SEM, you’re typically testing models (via changing the paths) against each other to see how well they recreate the means and covariance structure of the data relative to how complex the model is. This approach is a little different from something like regression where you may be interested in finding a subset of variables that best predict an outcome or maximize R squared.
I hope this helps. The resources I provided will have considerably more depth than what I was able to provide here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: what are the right or common steps to successfully build a structural equation model?
Hi,
I am sorry to see that you have not received a reply yet. One reason for this is that SEM is relatively new to the community of JMP users.
I think it might also help if you could post a single question in your post. Discussion posts that are short and specific requests tend to get the best response. Posting the simplest possible example data to illustrate what you are trying to do is also a good thing in most cases.
I know a little about SEM (it was one of the modules in my Stats MSc). From what I know, I think it is hard to give a prescription for "the right way" to build a structural equation model. I don't know enough to comment on the approach that you have proposed. I would say that 50 variables is a lot more than I have seen in SEM examples, so this might be difficult.
In terms of resources, you should look for anything by Laura Castro-Schilo (@LauraCS). For example,
Also, my colleague, @jordanwalters, is posting articles about SEM every month in the JMPer Cable. Jordan might have some suggestions for resources that he found useful when learning about SEM.
Sorry I couldn't really answer your questions. But I hope this helpful.
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: what are the right or common steps to successfully build a structural equation model?
Hi lujc07,
Resources for SEM:
I highly recommend seeking out some of Laura's (@LauraCS) resources and posts as a good starter for using SEM in JMP.
A good one to watch is: https://community.jmp.com/t5/Discovery-Summit-Americas-2020/ABCs-of-Structural-Equations-Models-2020...
Additionally, there are a number of good SEM texts out there, I think a good starter is "Principles and Practice of Structural Equation Modeling" by Rex Kline, it has an applied bent to it. Other authors you'll see are Ken Bollen, Schumacker & Lomax, Rick Hoyal, and many others; all their texts are great resources as well and some will be more technical than others. Most of the texts will likely use examples from education and social science's but the approaches apply generally. The technique is simply used widely in those areas.
Re: Q2: I think it'd generally be considered most appropriate for SEM to follow Exploratory Factor Analysis (EFA / FA) as opposed to some of the other dimension reduction techniques you listed (PCA, clustering, etc.). However, if you're reading literature, you might see other ones like PCA being used prior. A useful ordering in your head for thinking about it might be Correlation Matrix -> EFA -> CFA -> SEM.
Re: Q1: Steps 1-6 are a good general set of steps for moving into SEM. In fact, I think sometimes people forget these important earlier steps and just try to build a model right away which can lead to headaches. A couple of suggestion I have:
Step 5:
run factor analysis for each group. In each group, I selected 2-3 variables that have high and similar loadings in the same factor as indicators for a latent variable (this step tends to be subjective).
In your FA step I would consider including all the variables (v1-v9 etc) associated with your latent variables "water, air, and habitat" in the FA (you possibly did this but I wasn't quite sure). The reason is, it will help you identify those variables that may cross load with these other factors and help you decide if you want to include them or not. An item may look great when it’s on its own in a small subset but when it’s included with the other variables it may not be one that you want to retain. It will also help you see if these factors are separating out as you'd expect.
Additionally, use at least 3 variables for a latent variable (good rule of thumb) and if you have more than that, that are appropriate, and load well onto a factor (such as 4 or 5) bring those along as well no need to toss them out if they measure the construct well. If you're in the position of having enough data just note it is ideal if you can do EFAs on part of the data (a test set) and then follow-up with CFAs on another set of data (a validity set). The factor structure for the EFAs is going to be driven by the data and following it up with CFAs on a new set of data will help you identify if the item parameters and factors replicate well.
Step 6:
- 6. run confirmatory factor analysis with selected variables (see diagram below). If pass (based on fit indices, indicator reliability, composite reliability, construct maximal realiability, construct validity matrix), use these latent variables to build structural equation model with observed variables (human development, animal group). If not pass, change the combination of variables until pass.
After you've settled on your variables for your latent variables (using all the information you noted in your post) and the observed variables you want to use then think about the different SEMs you want to test. The goal of SEM is to use theory or more generally your knowledge of an area to test out multiple competing models. A competing model is one that differs in its parameterization. For a simple example, if you removed the path between "Human Development 2" and "Habitat" that would result in a new, slightly simpler model that you could test (a nested model). The model differs by 1 parameter and would result in a new set of fit indices and results. If that model fits practically as well as the model that included that path we might conclude there is statistical evidence for it being a more parsimonious model that fits just as well as a more complex one. You can expand on this idea and run multiple models until you settle on your model that exhibits good fit and is reasonable for your theory. When modifying your model to try other models, I recommend being intentional with your changes to paths, and testing things that would make sense to you and the theory your interested in.
In SEM, you’re typically testing models (via changing the paths) against each other to see how well they recreate the means and covariance structure of the data relative to how complex the model is. This approach is a little different from something like regression where you may be interested in finding a subset of variables that best predict an outcome or maximize R squared.
I hope this helps. The resources I provided will have considerably more depth than what I was able to provide here.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us