- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- unique variance for each variable in multiple regression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
unique variance for each variable in multiple regression
In the attached dataset and screenshot, I am trying to find the effect of prior academic achievement and SES on current achievement for students. How could I find the unique variance/semipartial correlation for each variance? I know it is not the square of standard beta for the variable. Any ideas? Thank you!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: unique variance for each variable in multiple regression
JMP doesn't report semipartial correlations directly, but they can be calculated from regressions.
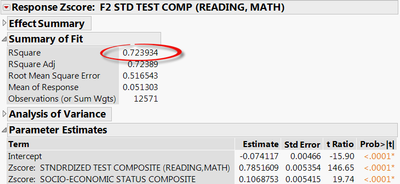
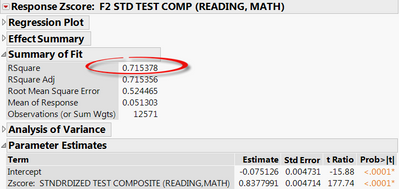
For example, to get the semipartial correlation for socioeconomic status, first, run two regressions as shown in the screenshots.
Then take the sqrt of the difference in RSquare values between the two models, i..e. sqrt(0.723934-0.715378)=0.0925. This indicates the "unique" contribution of socioeconomic status as a predictor.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: unique variance for each variable in multiple regression
JMP doesn't report semipartial correlations directly, but they can be calculated from regressions.
For example, to get the semipartial correlation for socioeconomic status, first, run two regressions as shown in the screenshots.
Then take the sqrt of the difference in RSquare values between the two models, i..e. sqrt(0.723934-0.715378)=0.0925. This indicates the "unique" contribution of socioeconomic status as a predictor.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us