- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: how to compare the shape of curves vs a baseline in JMP?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
how to compare the shape of curves vs a baseline in JMP?
Hi there
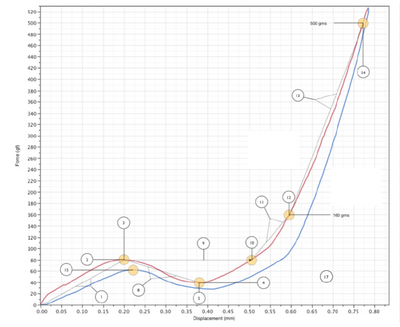
We are trying to evaluate the differences between measured data against an ideal baseline; in this case we're comparing the shape / magnitdue / quality of force displacement curves.
We've in the past compared the various slopes, peaks and valleys to do this, but are finding this doesnt capture all the variation we are seeing.
Is there a way to compare the entire "shape" of one curve against that of a baseline (for example comparing red vs blue in my attached plot)?
thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to compare the shape of curves vs a baseline in JMP?
Is your goal to just characterize the magnitude of the delta at various locations along the x axis? If so I'd just create a simple run chart at predetermined x values and find the delta between one curve and the other. That will capture turning points, magnitude of delta, etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to compare the shape of curves vs a baseline in JMP?
I think there a multiple ways that you could compare a 'master' curve to others. Some are more exploratory data analysis based like the correlation...some are more modeling based so I think some thought around what your criteria are for comparison is warranted before we offer more specific guidance. And also perhaps some insight around the practical purpose of the comparison and what decisions or actions it would lead to is helpful. Is it to explain, predict or something else? Reason I'm bringing all this up is the famous Anscombe's Quartet data set has 'curves' if you will, that have many identical 'statistics'...but the insight from each element of the quartet are very different. See Anscombe.jmp which is in the JMP Sample Data Directory.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to compare the shape of curves vs a baseline in JMP?
If I'm interpreting your question correctly then the Functional Data Explorer in JMP Pro is likely what you're looking for.
Here are some resources for learning more about the Functional Data Explorer:
- Mastering JMP webcast on using the Functional Data Explorer
- Video demonstration from @Peter_Hersh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to compare the shape of curves vs a baseline in JMP?
@abdulj, a sanitized (all IP removed) data table for the data representing your two curves would be a good example to test several of the options for the Functional Data Explorer platform, for example DTW, dynamic time warping, and column functions, etc.
If possible and you have time please post.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to compare the shape of curves vs a baseline in JMP?
Sure - see attached table with a script to show the graph. Basically how can i quantify how different each of these curves are from one another. And if I designated one of these curves as a "master", how can compare how closely each of the other ones compares to the master?
thanks again!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to compare the shape of curves vs a baseline in JMP?
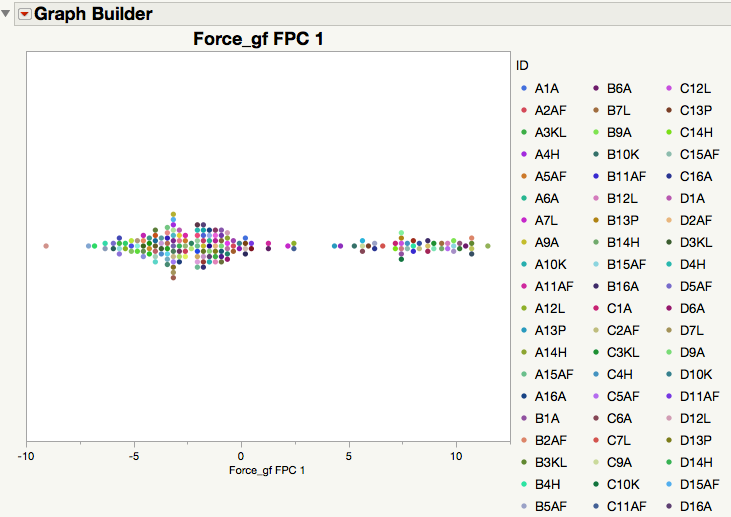
I did this in just a few minutes with Functional Data Explorer, FDE (requires JMP Pro 14) and without knowing your data, so it's not in any sense definitive. But it does confirm Jeff's suspicion that this might be an approach worth investigating.
It looked like ID1, ID2 and ID3, taken together, identify a unique trace. Using FDE showed that the first functional principal component accounted for nearly 95% of the variability between the traces, so might be a good measure of similarity or distance:
Take a look at the scripts within the updated table.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
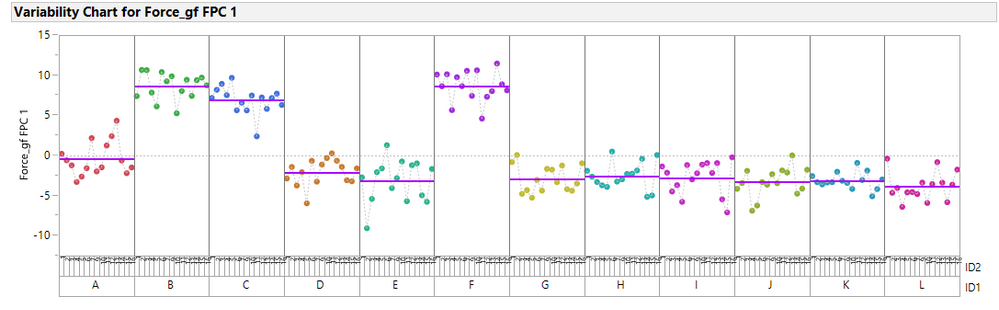
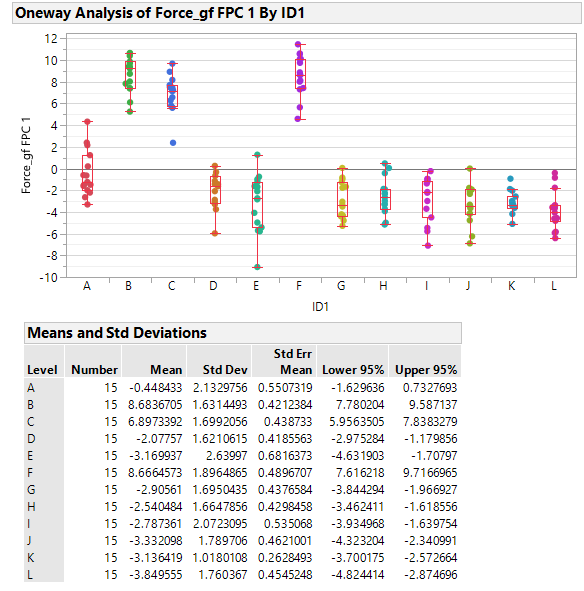
Re: how to compare the shape of curves vs a baseline in JMP?
This is just a different view of the @ian_jmp's results: a variability plot, and a bivariate of Force_gf FPC1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to compare the shape of curves vs a baseline in JMP?
Thanks @ian_jmp and @gzmorgan0
I'll look at this tool a bit deeper and let you know if i have any trouble.
Quick question - how is this different than using the standard Principal Components platform?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to compare the shape of curves vs a baseline in JMP?
I think you will find the answer to that in the resources that @Jeff_Perkinson shared.
But, briefly, this is a functional principal components analysis. One of way of thinking about functional principal components is that they are characteristic curves that describe the variation from the mean curve.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us