- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Why Is This a Cringeworthy Statistics Statement? #1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Why Is This a Cringeworthy Statistics Statement? #1
I'm going to start a few discussion threads over the next few weeks, and I invite any JMP user to chime
in with their thoughts. These discussions will revolve around "Cringeworthy Statistics Statements."
Please consider contributing. After a few days, I'll summarize thoughts in a blog post, and introduce another Cringeworthy Statement!
Here is Cringeworthy Statement #1:
We run a t-test to compare the means of two populations. We want 95% confidence in the results. We run the test, and the p-value comes back at 0.63. We make the statement "Since p is not less than 0.05, we conclude that there is no difference in the means of these populations."
Why is this statement Cringeworthy????
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why Is This a Cringeworthy Statistics Statement? #1
I agree with this example of cringeworthiness - classic misunderstanding of the absence of evidence not meaning evidence of absence. Please consider the classic, but less straightforward: "the 95% confidence interval ranges from x to y, meaning that I am 95% confident that the true effect is between x and y." I happen to believe it is fine to say that, even though I know the correct statement is that "95% of all random samples constructed this way will contain the true effect." Of course, we don't know if our sample is one of those 95% or one of the 5% that don't contain the true population effect, and it either does or does not. But, given the one sample we have, I think the best we can say is the first quoted statement, despite it technically not being correct.
I'd like to hear what other people think of this example. Statisticians love to point out how this wrong interpretation of the confidence interval is common, while I can completely understand it. And I confess to giving students the liberty to wrongly interpret it (though at least I point out what the correct interpretation is). The problem with the correct interpretation is that it doesn't leave us able to say anything about the sample we actually have.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why Is This a Cringeworthy Statistics Statement? #1
I wouldn't call the interpretation: "I am 95% confident that the sample mean difference is not less than Lower CI and not more than Upper CI" 'wrong' per se, in fact I think it's a perfectly appropriate way of phrasing it that stands "correct" and easily phrased, but I would say that the interpretation is just "commonly misunderstood" @dale_lehman as you point out.
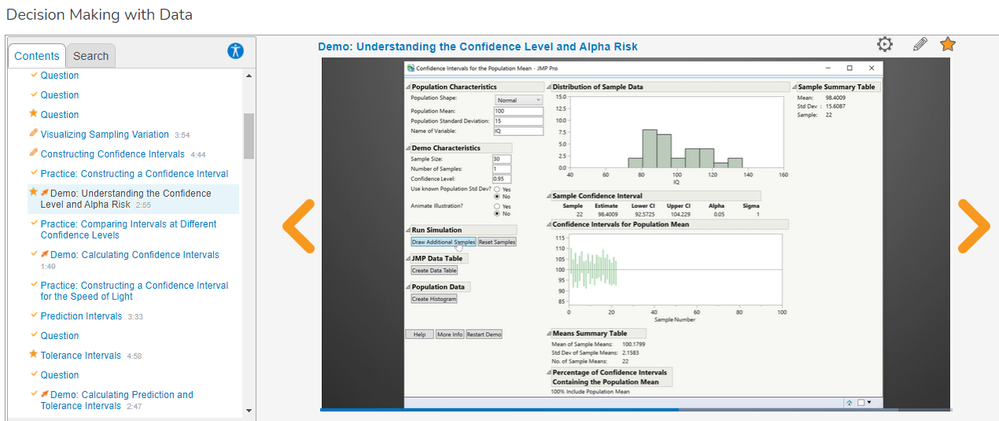
As @julian says in Decision Making with Data (STIPS) - Section 4.1 Estimation {and you can get this from the Transcript where I have screen grabbed the appropriate module reference below entitled "Demo: Understanding the Confidence Level and Alpha Risk"}
"We'll click Reset Samples, change the number of samples to 100, and click Draw Additional Samples. As we continue to draw samples, notice that the mean of the samples is close to the true mean. Also notice that close to 95% of the confidence intervals contain the true mean IQ value, and about 5% of the confidence intervals don't include the true mean."
"This is what we mean by the term "confidence." On average, for a 95% confidence interval, 95% of the time this interval method is used, the interval captures the true parameter value."
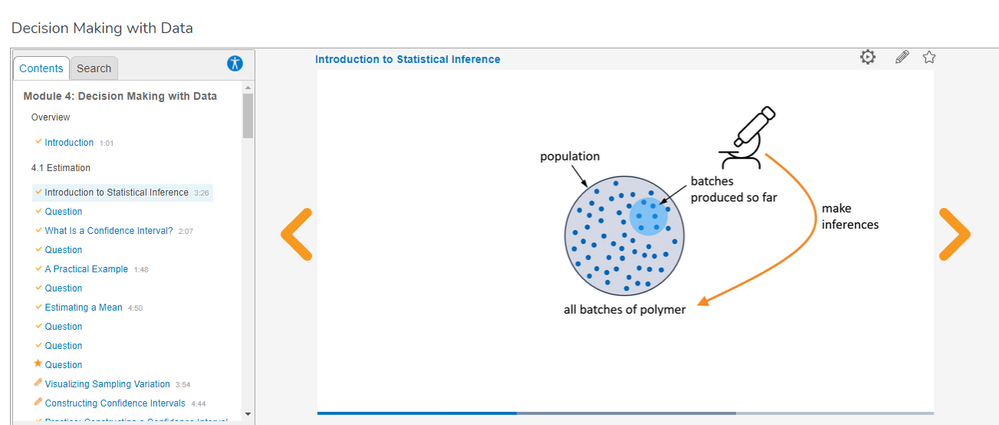
Of course, the inference is on the population, but it's based on the sample data. This is what we are doing when we are doing inferential statistics in general. The whole enterprise is about making inferences on the population based on the sample data that we have. Again, in the same Decision Making with Data Module 4, Watch Section 4.1 Introduction to Statistical Inference. Here, @mia_stephens speaks about this in a clear, precise and direct way.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why Is This a Cringeworthy Statistics Statement? #1
Where do I start? Sample size (none stated...might just be too small to give the signal a chance to rise above the noise)? What is the chosen alpha risk ('...95% confident in the results...' is a meaningless statement wrt to alpha risk. What does that statement even mean)? What is the null hypothesis (none stated)? What is the measurement error (known or even assumed)? What was the sampling plan (random, convenience, first/last off the line, stratified or some other plan)? What's the representation risk...not just the statistical risk? And on and on.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why Is This a Cringeworthy Statistics Statement? #1
Hey @P_Bartell ! Good to hear from you!
Thanks for the reply!! We'll put these ideas in my (growing) list of cringeworthy statements, and bring them up in future posts!
Stay well, my friend!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why Is This a Cringeworthy Statistics Statement? #1
I'll play...My favorite is actually quite simple...Using the phrase "statistically significant" applied anywhere without context. It's interesting that if you ask someone if they are more likely to believe something when the phrase statistically significant is added they answer yes without knowing anything about the comparisons being made.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why Is This a Cringeworthy Statistics Statement? #1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why Is This a Cringeworthy Statistics Statement? #1
+ No mention of a check for normality
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why Is This a Cringeworthy Statistics Statement? #1
To widen the discussion a little - to me this does not sound cringeworthy from the beginning. In my opinion it can still be a valid decision. Of course, as others pointed out already, there may be missing a lot of additional information to trust that decision. So to my eyes it depends on the context of the statement, and who put it. And what, by the way, would be the right statement with the same number of words?
Also, although I like sometimes discussions about right wording - terms are important, I don't like building up a wall between statisticians and process engineers that do not have that deep knowledge in statistics. But the latter know their data and processes. And as we can imagine, there are a lot of things that are even more important beneath the bare table of numbers. This could be environment of data sampling as well as consequences of the decision made, like @P_Bartell stated already. Decisions still have to be made by humans, not by machine.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why Is This a Cringeworthy Statistics Statement? #1
I am really fond of @Georg 's last sentence in his reply above. As a statistician working on process/product commercialization or corrective action teams for 20+ years in industry, I would often tell the engineers and scientists and managers I worked with, "The day you let me, a statistician, tell you how to run your processes is the day your road to ruin begins. You've forgotten more about your processes/products than I'll ever know."
Or as Walter Shewhart wrote (paraphrased by me) : "The long range contribution of statistics depends not so much on creating a bunch of statisticians as it does in creating a group of statistically minded engineers, scientists, production personnel and others."
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us