- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- When forcing intercept to zero, why JMP does not provide R-squared?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
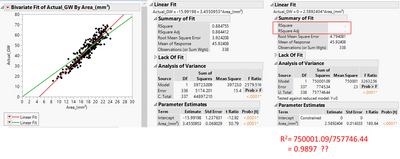
When forcing intercept to zero, why JMP does not provide R-squared?
Hello, I have some questions.
When I have a linear model in JMP, I want to force intercept to zero.
So, In Fit Special, I chose "Constrain Intercept to 0" then I got the new output from JMP.
My questions are
1) why JMP does not provide R-squared when intercept becomes zero?
2) R-squared is calculated by SSR/SST, can I calculate R-squared by myself using the data JMP provides? If I calculated by myself, it's higher than before. Is this possible? In this case, it says R-squared is 99%. Can I say this R-squared is correct?
Thanks,
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When forcing intercept to zero, why JMP does not provide R-squared?
This case is one of "just because you can doesn't mean you should."
Yes, the sum of squares that are normally used to compute R square are provided. But the resulting ratio has no meaning. R square is called the "coefficient of determination" in linear regression. When R square equals 1, then all the variation in Y is explained or determined by variation in X. (That is not a statement about causation.) When R square equals 0, then Y is independent of X. It is, therefore, the mean of Y for all X. But your null hypothesis is that Y = 0. So the ANOVA might be statistically significant, but the R square is undefined.
See this article for more information.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: When forcing intercept to zero, why JMP does not provide R-squared?
This case is one of "just because you can doesn't mean you should."
Yes, the sum of squares that are normally used to compute R square are provided. But the resulting ratio has no meaning. R square is called the "coefficient of determination" in linear regression. When R square equals 1, then all the variation in Y is explained or determined by variation in X. (That is not a statement about causation.) When R square equals 0, then Y is independent of X. It is, therefore, the mean of Y for all X. But your null hypothesis is that Y = 0. So the ANOVA might be statistically significant, but the R square is undefined.
See this article for more information.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us