- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Wald p value not shown in JMP version 12
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Wald p value not shown in JMP version 12
I am currently using JMP 12 for my analysis . I need technical inputs on following aspect
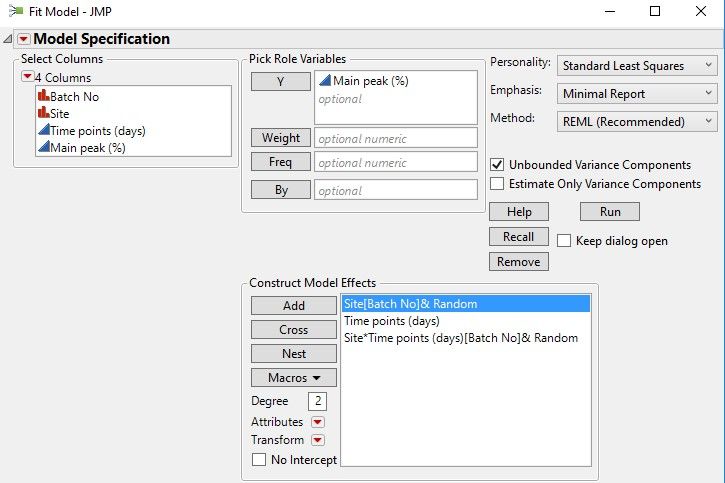
- I am using mixed effects model to assess whether the difference between sites is significant
- I would like to know the wald p value corresponding to Random effect Site *time [batch] to infer whether impact is significant or not
Please let me know if there is any possibility see wald p value info in version 12 . If there is no option please let me know the formula or procedure that can be used to calculate the wald p value
Is it possible to share script for generating wald p value in JMP version 12
Looking forward for your assistance in this regard as soon as possible as its critical for our project
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Wald p value not shown in JMP version 12
Hi @Dinesh,
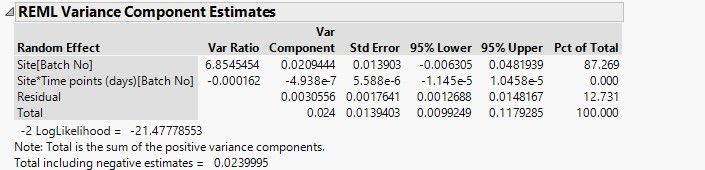
Sure thing. That p-value is calculated with Z as the reference distribution, and the Variance Components table has all the ingredients to get the test statistic. You can save the table yourself (right click > make into data table), and then make two new columns, the ratio of the variance component to the standard error, and then a second column, a lookup of that quotient in the z-distribution, with some simple arithmetic to find the proportion more extreme than that value in the reference distribution. Here's an example of that:
Names Default To Here( 1 );
dt = Open( "$SAMPLE_DATA\Cholesterol Stacked.jmp" );
platform = dt << Fit Model(
Y( :Y ),
Effects(
:Treatment,
:Month,
:Name( "AM/PM" ),
:Treatment * :Month,
:Treatment * :Name( "AM/PM" ),
:Month * :Name( "AM/PM" ),
:Treatment * :Month * :Name( "AM/PM" )
),
Random Effects(
:Patient[:Treatment],
:Patient * :Month[:Treatment],
:Patient * :Name( "AM/PM" )[:Treatment],
:Patient * :Month * :Name( "AM/PM" )[:Treatment]
),
NoBounds( 1 ),
Personality( "Standard Least Squares" ),
Method( "REML" ),
Emphasis( "Minimal Report" ),
Run(
:Y << {Summary of Fit( 1 ), Analysis of Variance( 0 ), Parameter Estimates( 1 ), Lack of Fit( 0 ),
Scaled Estimates( 0 ), Plot Actual by Predicted( 0 ), Plot Regression( 0 ),
Plot Residual by Predicted( 0 ), Plot Studentized Residuals( 0 ), Plot Effect Leverage( 0 ),
Plot Residual by Normal Quantiles( 0 )}
)
);
Wait( 0 );
Report( platform )[Outline Box( "Response Y" )][Outline Box( "REML Variance Component Estimates" )][
Table Box( 1 )] << Make Into Data Table;
Report( platform ) << Close Window;
New Column( "Var Component/Std Error",
Numeric,
"Continuous",
Format( "Best", 12 ),
Formula( :Var Component / :Std Error ),
Set Selected
);
New Column( "Prob > |Z|",
Numeric,
"Continuous",
Format( "Best", 12 ),
Formula( (1 - Normal Distribution( :Name( "Var Component/Std Error" ) )) * 2 ),
Set Selected
);
This will return the following (showing JMP 14 so you can see JMP's calculation of the Wald P-value, which you can confirm is the same as the one calculated in the method I described above).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Wald p value not shown in JMP version 12
Help==>Books==>Fitting Linear Models
it states for Fitting Standard Least Square models
Wald p-Value Gives the p-value for the test that the covariance parameter is equal to zero.
This column appears only when you have selected Unbounded Variance Components in
the Fit Model launch window.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Wald p value not shown in JMP version 12
inspite of selecting unbound variance component in fit model launch window
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Wald p value not shown in JMP version 12
Hi @Dinesh,
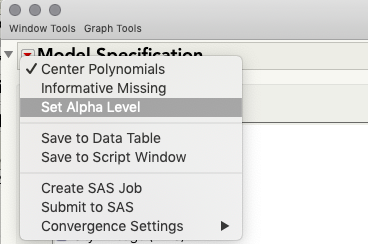
P-values are not displayed for variance components in JMP 12; these p-values were added in JMP 13. I realize it's not exactly what you're looking for, but you can use the confidence intervals in much the same way as the hypothesis test at an alpha of 1-confidence level by looking to see if 0 is contained in the interval. If it is not, your p-value (for the corresponding hypothesis test) is < 1-confidence level. If you need to change this confidence level, you can do that when you launch Fit Model: click the top red triangle in the launch window > Alpha Level.
I hope this helps some!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Wald p value not shown in JMP version 12
script specifically to generate this wald p value . We had used used jmp
trial 14 while writing protocol and committed to include wald p value in
results .
But now we have licensed only for 12 . So to bind to that protocol , we
have to include wald p value in report . It would be of great help if you
can share the same .
Thanks a lot again for your inputs
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Wald p value not shown in JMP version 12
Hi @Dinesh,
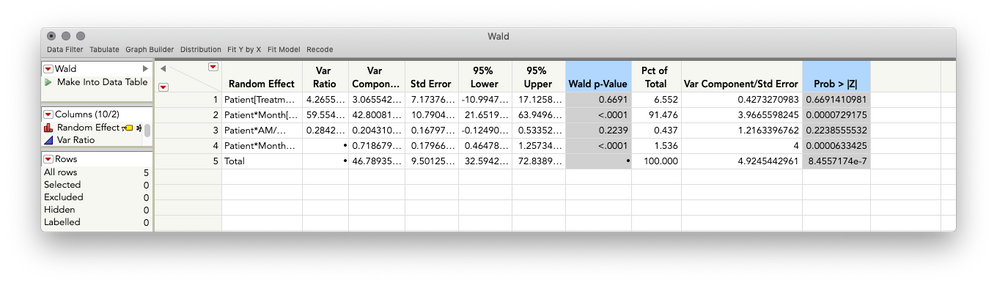
Sure thing. That p-value is calculated with Z as the reference distribution, and the Variance Components table has all the ingredients to get the test statistic. You can save the table yourself (right click > make into data table), and then make two new columns, the ratio of the variance component to the standard error, and then a second column, a lookup of that quotient in the z-distribution, with some simple arithmetic to find the proportion more extreme than that value in the reference distribution. Here's an example of that:
Names Default To Here( 1 );
dt = Open( "$SAMPLE_DATA\Cholesterol Stacked.jmp" );
platform = dt << Fit Model(
Y( :Y ),
Effects(
:Treatment,
:Month,
:Name( "AM/PM" ),
:Treatment * :Month,
:Treatment * :Name( "AM/PM" ),
:Month * :Name( "AM/PM" ),
:Treatment * :Month * :Name( "AM/PM" )
),
Random Effects(
:Patient[:Treatment],
:Patient * :Month[:Treatment],
:Patient * :Name( "AM/PM" )[:Treatment],
:Patient * :Month * :Name( "AM/PM" )[:Treatment]
),
NoBounds( 1 ),
Personality( "Standard Least Squares" ),
Method( "REML" ),
Emphasis( "Minimal Report" ),
Run(
:Y << {Summary of Fit( 1 ), Analysis of Variance( 0 ), Parameter Estimates( 1 ), Lack of Fit( 0 ),
Scaled Estimates( 0 ), Plot Actual by Predicted( 0 ), Plot Regression( 0 ),
Plot Residual by Predicted( 0 ), Plot Studentized Residuals( 0 ), Plot Effect Leverage( 0 ),
Plot Residual by Normal Quantiles( 0 )}
)
);
Wait( 0 );
Report( platform )[Outline Box( "Response Y" )][Outline Box( "REML Variance Component Estimates" )][
Table Box( 1 )] << Make Into Data Table;
Report( platform ) << Close Window;
New Column( "Var Component/Std Error",
Numeric,
"Continuous",
Format( "Best", 12 ),
Formula( :Var Component / :Std Error ),
Set Selected
);
New Column( "Prob > |Z|",
Numeric,
"Continuous",
Format( "Best", 12 ),
Formula( (1 - Normal Distribution( :Name( "Var Component/Std Error" ) )) * 2 ),
Set Selected
);
This will return the following (showing JMP 14 so you can see JMP's calculation of the Wald P-value, which you can confirm is the same as the one calculated in the method I described above).
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us