- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Use of Logistic 3 Parameter (L3P) model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Use of Logistic 3 Parameter (L3P) model
Hi,
We're looking at some biological data representing an amplification which we're using JMP to fit the L3P model to
- and are thereby obtaining the growth rate, asymptote and inflection point on the sigmoid curves which result.
We're then using the growth rate parameter specifically in an ANOVA test to detect whether the curves (ie the biological test) are adversely affected by challenges, under the expectation of an adverse challenge resulting in us rejecting the null hypotheis.
The problem that I'm experiencing is that the more adverse the challenge - the greater the likelihood of either some or all of the assays not working (curves not being generated).
When this occurs, I cannot obtain the 3 parameters which I'm using in ANOVA and so am somewhat stuck on how to handle this particularly informative data.
The pattern (with increasing challenge) is of increasing variability in the curve that is modelled (towards flat lining) and then increasing numbers of failed amplifications (actual flat lines) with severity of challenge - which culminate in all replicates actually flat lining and no curve fit being possible.
Thanks for the help.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of Logistic 3 Parameter (L3P) model
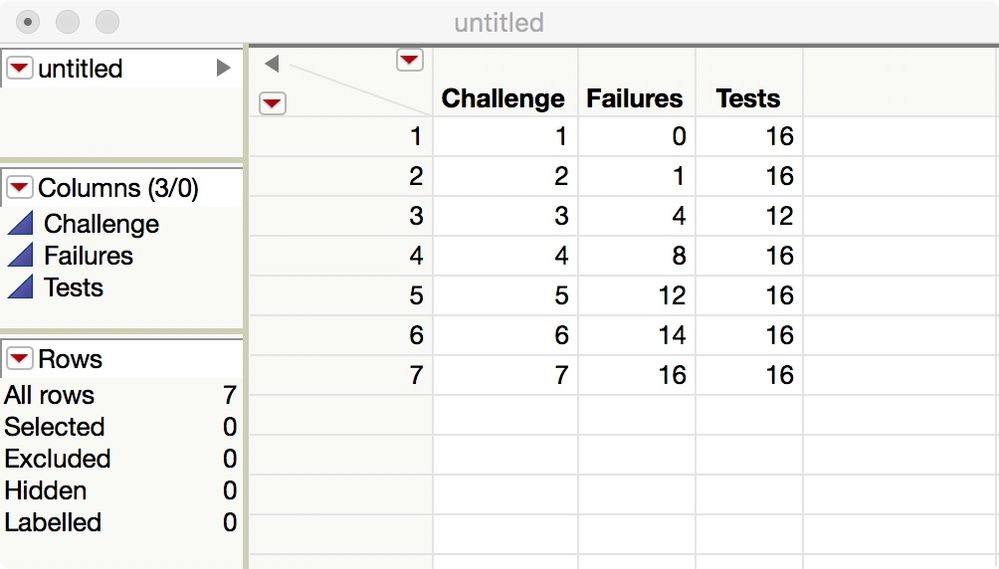
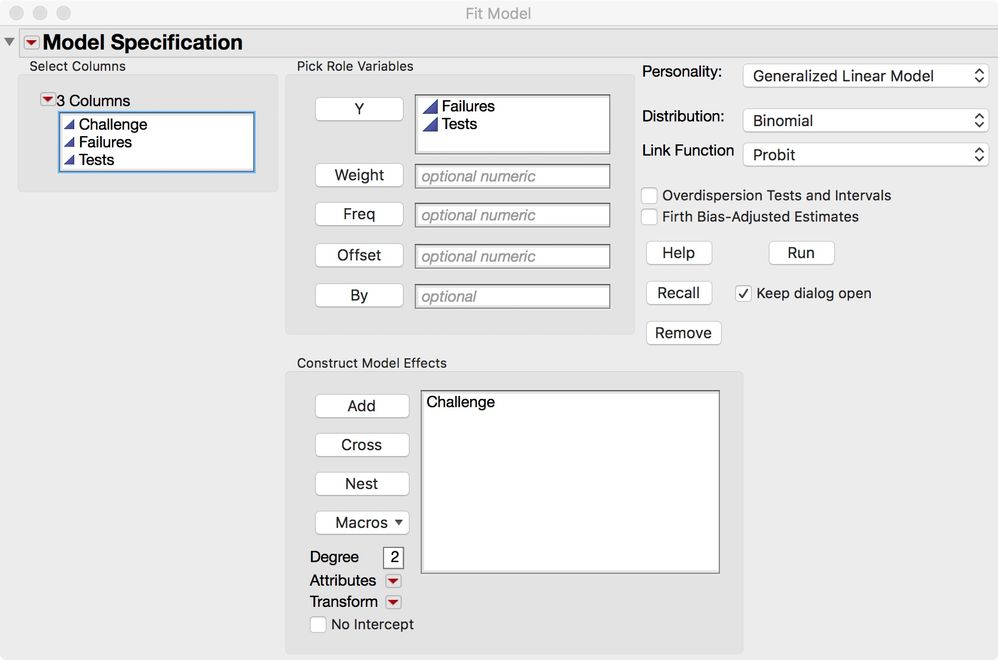
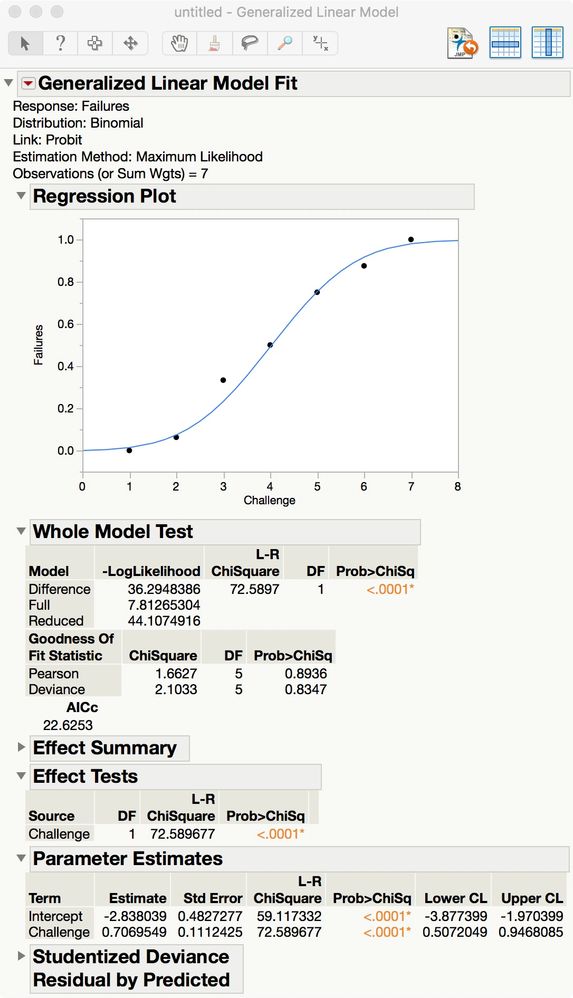
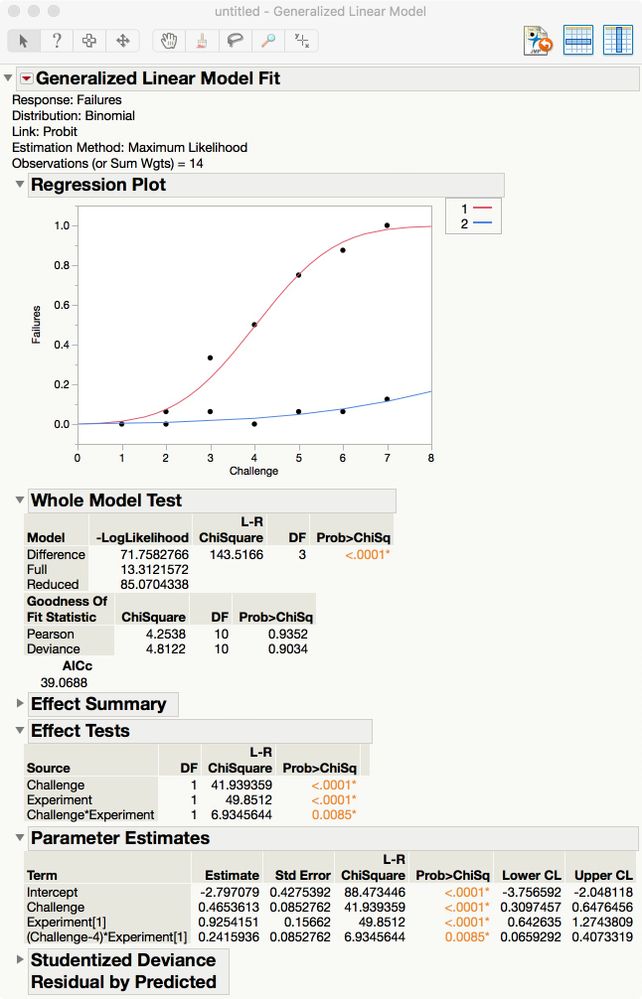
You could analyze such a table (challenge, number of failures, total number of tests - 16) using a probit model.
Select Analyze > Fit Model. Select both the Failures and Tests data columns and click Y. (Be sure to enter them in that order.) Select the Challenge data column and click Add. Click Standard Least Squares and select Generalized Linear Model. Select the Binomial distribution and the Probit link function.
Click Run.
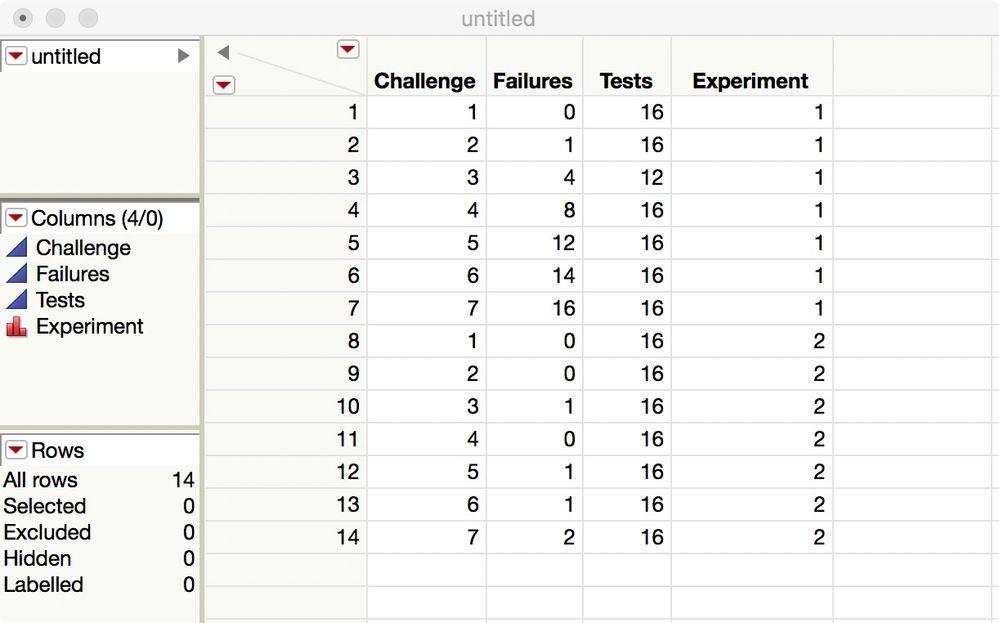
You can extend this analysis to include the experiment.
Add Experiment as two effects: the main effect and crossed with Challenge.
The estimates can be used to test the significance of the effects and the model can be used to predict.
The Experiment example here could be another categorical or continuous factor. There could be multiple factors in the probit model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of Logistic 3 Parameter (L3P) model
Your continuous factor is challenge. Perhaps your factor range is too aggressive and leads to non-responses. The point of the experiment is to model the data and test the parameter estimates. Can you shift the factor range lower? For example, if challenge was 50-100, try 25-75? That way you might be able to get more usable data for your model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of Logistic 3 Parameter (L3P) model
Hiya,
Many thanks for the response and I think I understand.
The problem is that we are required to test the assay to failure and so our data ranges from perfectly superimposed replicate sigmoidal curves in all cases (with little challenge) at one end
- through (at the other end) - to perfectly superimposed replicate flat lines.
Between these two extremes there's a pattern of increasing sporadic failures in replicate samples.
I was thinking that if I grouped all of our replicates (by challenge) together into generating just one curve - then as long as we've at least one successful sigmoidal curve, that we'll be able to obtain the 3 parameters on each challenge ie will be able to perform a valid curve fit.
The problem though that then arises - is that instead of having values for the growth rate, inflection point and asymptote in each replicate - that we then have just 1 value for all replicates - and I'm not too sure how to take this one value through to t testing, (M)ANOVAs and equivalence testing because it's the actual replicate values themselves that're required to perform this type of analysis.
My next line of thinking was to use the summary data which JMP delivers on mean, SE and confidence intervals on that single 'summary' sigmoidal curve and to attempt to perform an ANOVA from Data Summary Table ie by simply lifting mean and SE out of the 'By group' L3P fit and attempting this procedure (which you've been kind enough to supply):
https://community.jmp.com/t5/JMP-Scripts/ANOVA-from-Data-Summary/ta-p/21487
What worries me a little is whether this form of grouping of 'flat line' data with actual sigmoidal curve data will invalidate some underlying assumption ie will change the nature of the curve. The inflexion point is a constant in our curve fitting exercise, and so I'm wondering whether this 'by group' approach will alter the inflexion point away from where we expect it to be.
Genuinely appreciate the help!
Thanks. C.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of Logistic 3 Parameter (L3P) model
So - the data we might observe might look like (illustrated with 16 replicates):
challenge units - successful curve fit - unsuccessful curve fit*
-------1------------------16---------------------00-----
-------2------------------15---------------------01-----
-------3------------------12---------------------04-----
-------4------------------08---------------------08-----
-------5------------------04---------------------12-----
-------6------------------02---------------------14-----
-------7------------------00---------------------16-----
However the next experiment might look like:
challenge units - successful curve fit - unsuccessful curve fit*
-------1------------------16---------------------00-----
-------2------------------16---------------------00-----
-------3------------------15---------------------01-----
-------4------------------16---------------------00-----
-------5------------------15---------------------01-----
-------6------------------15---------------------01-----
-------7------------------14---------------------02-----
* no reaction occurring
So - the first experiment feels as though it lends itself to a binary outcome, and the second to quantitative outcome (increased variability in sigmoid curves with challenge as assessed by asymptote/growth rate) - however, I somehow need to roll the two together into one test.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of Logistic 3 Parameter (L3P) model
You could analyze such a table (challenge, number of failures, total number of tests - 16) using a probit model.
Select Analyze > Fit Model. Select both the Failures and Tests data columns and click Y. (Be sure to enter them in that order.) Select the Challenge data column and click Add. Click Standard Least Squares and select Generalized Linear Model. Select the Binomial distribution and the Probit link function.
Click Run.
You can extend this analysis to include the experiment.
Add Experiment as two effects: the main effect and crossed with Challenge.
The estimates can be used to test the significance of the effects and the model can be used to predict.
The Experiment example here could be another categorical or continuous factor. There could be multiple factors in the probit model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of Logistic 3 Parameter (L3P) model
Many thanks for that - and it's almost exactly :) what we're currently doing (GLM personality-Binomial distribution-Probit link) when we examine the data we generate only for whether the assay has worked or failed.
We're not there looking at any parameter other than whether the assay has worked or whether it hasn't.
We were though hoping to perform an analysis which is more discriminating.
We're striving to use a method for assessing how the assay degrades (without explicitly failing although failure may occur) as we increase the level of challenge.
So - we often obtain data of this form:
challenge units - successful curve fit - unsuccessful curve fit*
-------1------------------16---------------------00-----
-------2------------------16---------------------00-----
-------3------------------16---------------------00-----
-------4------------------16---------------------00-----
-------5------------------16---------------------00-----
-------6------------------16---------------------00-----
-------7------------------16---------------------00-----
If we were to fit a Log 3 Parameter model to each of the sigmoid curves in the 16 replicates x 7 conditions above - we discover that as the challenge increases from 1 to 7 - that there's a decrease in growth rate and a decrease in upper asymptote (ie in 2 of the 3 parameters generated by the L3P model).
So - as long as the assay works and a model fit is possible - with increasing challenge we see a no change in inflection point, a decrease in upper asymptote and a decrease in growth rate) which is great.
All of our problems arise when we're 'between' these 2 statistical techniques; by that I mean when a sporadic (or more) failures eg
challenge units - successful curve fit - unsuccessful curve fit*
-------1------------------16---------------------00-----
-------2------------------16---------------------00-----
-------3------------------15---------------------01-----
-------4------------------16---------------------00-----
-------5------------------15---------------------01-----
-------6------------------15---------------------01-----
-------7------------------14---------------------02-----
occur - as no Log 3 P model can be generated in these few (ie five in the table above) assays.
I have been wondering whether we could use the baseline value (ie close to zero) for the upper asymptote, 0 for the growth rate and 'missing data' for the inflection point in the case of failures ie in those 5 cases - such that we'd have data to take forwards in failed assays for use in (m)ANOVA-like tests of differences between challenge severity.
On the one hand it feels like a positive move to do this as no data is discarded, however I'm unsure whether I'm contravening rules of normality (required in (m)ANOVA-like tests) by assigning failed assays values of zero and then using them. Although we do sometimes obtain L3P fits to failed reactions (poor R2 values) - the 3P values returned do not make sense, are often extreme outliers - and so must be deleted if we're to pursue difference between group testing by using them.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us