- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Two-way ANOVA with randomized complete block design in JMP?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Two-way ANOVA with randomized complete block design in JMP?
I am trying to perform an ANOVA on a set of data with three variables: sample method (two different methods), chemicals (three different chemicals), and groundwater wells (12 different wells). It is a randomized compete block design, as both methods and all three chemicals are tested from each well.
I want to set this up as a two-way (method and chemical) with the wells as blocks. I see the ability to designate blocks in the one-way ANOVA setup, but no way to designate this in the two-way ANOVA setup. I know this is possible in SAS, but I do not have access to that program and am trying to do this in JMP, if possible.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Two-way ANOVA with randomized complete block design in JMP?
It sounds like sample method and chemicals are measured factorially, which means for each Well you actually have 2 observations for each chemical, and 3 observations for each sample method (the hidden replication of a factorial design). This means certain additional terms are estimatable. The largest model would include as factors:
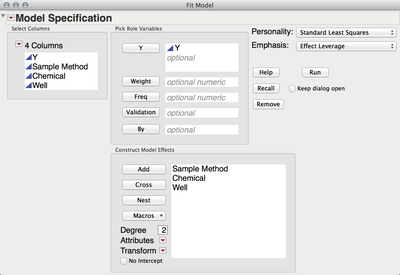
Sample Method, Chemicals, Sample Method x Chemicals, Well, Well x Chemical, Well x Sample method (but not the three way interaction, since that is not estimatable unless you have a full replication of the within-well factorial). This is like what Jeff showed above but with the interactions you can estimate. To define an interaction you can select a source in the model effects and another variable in the cols list to the left, then click "Cross".
In your case you have nearly a three way factorial -- you're missing only the highest order interaction. Since that's the case you can select all three variables in the list on the left of fit model, then go to "Macros" and select "Full Factorial" or "Factorial Sorted" -- the latter is my preference because it groups the terms starting with lower-order effects first. If you use one of these macros you will have an additional effect (the three way interaction) that you can't estimate, so you can simply delete it from the model effects list.
So why no three way interaction? The factorial combination of sample Method and chemical draw out a 2x3 = 6 cell design, so at each level of well you need at least 6 observations to estimate that structure. You gain the interactions of well x chemical, and well x sample method because you actually do have a replicates of chemical and sample method within a given well (they happen to be across the levels of another factor, but that's fine, the model estimates that offset). If you have a full design replication (e.g. 12 observations for each well, 2 for each combination of sample method and chemical) you gain the ability to estimate that three-way interaction since there is data on which to assess the "stability" of the two way interactions across the level of a third variable.
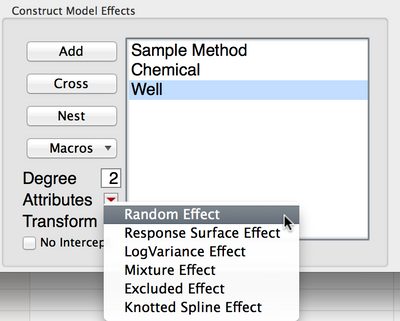
As for whether or not to treat well (and the interactions with well) as a random effect, I'd ask yourself whether you would choose these same wells if you were to replicate the study. If these wells in particular would be selected again, they're not random effects. If these wells are a subset of wells and a replication would lead to choosing different wells at random, then the estimates for well are random and the sources should be marked as so. This can be done by selecting the source in the effects list, then click "Attributes" and select "Random."
I hope this helps!
Julian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Two-way ANOVA with randomized complete block design in JMP?
I would also like to see the response to this question. I have had the same issue.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Two-way ANOVA with randomized complete block design in JMP?
If I'm understanding your question correctly, you just need to use Analyze -> Fit Model and add Sample Method, Chemical and Well as effects.
You could designate Well as a Random Effect using the Attributes menu but I don't think that's necessary.
-Jeff
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Two-way ANOVA with randomized complete block design in JMP?
It sounds like sample method and chemicals are measured factorially, which means for each Well you actually have 2 observations for each chemical, and 3 observations for each sample method (the hidden replication of a factorial design). This means certain additional terms are estimatable. The largest model would include as factors:
Sample Method, Chemicals, Sample Method x Chemicals, Well, Well x Chemical, Well x Sample method (but not the three way interaction, since that is not estimatable unless you have a full replication of the within-well factorial). This is like what Jeff showed above but with the interactions you can estimate. To define an interaction you can select a source in the model effects and another variable in the cols list to the left, then click "Cross".
In your case you have nearly a three way factorial -- you're missing only the highest order interaction. Since that's the case you can select all three variables in the list on the left of fit model, then go to "Macros" and select "Full Factorial" or "Factorial Sorted" -- the latter is my preference because it groups the terms starting with lower-order effects first. If you use one of these macros you will have an additional effect (the three way interaction) that you can't estimate, so you can simply delete it from the model effects list.
So why no three way interaction? The factorial combination of sample Method and chemical draw out a 2x3 = 6 cell design, so at each level of well you need at least 6 observations to estimate that structure. You gain the interactions of well x chemical, and well x sample method because you actually do have a replicates of chemical and sample method within a given well (they happen to be across the levels of another factor, but that's fine, the model estimates that offset). If you have a full design replication (e.g. 12 observations for each well, 2 for each combination of sample method and chemical) you gain the ability to estimate that three-way interaction since there is data on which to assess the "stability" of the two way interactions across the level of a third variable.
As for whether or not to treat well (and the interactions with well) as a random effect, I'd ask yourself whether you would choose these same wells if you were to replicate the study. If these wells in particular would be selected again, they're not random effects. If these wells are a subset of wells and a replication would lead to choosing different wells at random, then the estimates for well are random and the sources should be marked as so. This can be done by selecting the source in the effects list, then click "Attributes" and select "Random."
I hope this helps!
Julian
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us