- We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- JMP 19 is here! Learn more about the new features.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Space filling versus optimal DOE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Space filling versus optimal DOE
For mixtures frequently space filling DOE's are used; guess these are not optimal? So what is then the benefit?
Why not use space filling also for non-mixtures instead of Optimal DOE? I am preparing a DOE course and expect these questions and so far I don't have the right answers.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
Hi @frankderuyck,
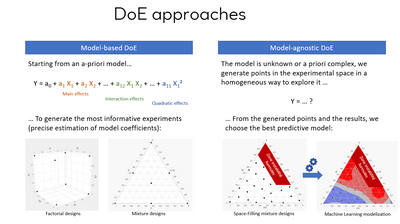
Space-filling designs and optimal designs (no matter if it is for mixture or other factors type, they can be used in both cases) are two completely different DOE mindsets: Model-based vs. Model-agnostic.
- Model-based : This type of designs of experiments involves postulating a specific model a-priori (with main effects, interactions terms, etc...), and then generating points in order to optimize the estimation of the model's coefficients. This approach assumes a specific model form and is useful when the underlying model is well-known or when there is prior knowledge about the system being studied. It may requires fewer points, and is particularly advised if you want to easily have access to explainable/interpretable results.
Example : My response Y is heavily influenced by statistically significants main effects from factor A and B, and by the statistically significant 2-factors interaction between A and B.
- Model-agnostic : This type of designs of experiments involves distributing points uniformly/homogeneously (and randomly) in the experimental space and then fitting different models to these points to obtain the best predictive model. This approach may require a high number of points depending on the complexity of the model tested (Regression, SVM, Neural Networks, Tree-based models,...), does not assume any specific model, and is useful when the underlying model is unknown or complex. But this approach may be sensitive to noise and the use of ML models may lead to overfitting situations...
Both approaches have their advantages and disadvantages. Model-agnostic designs can be more flexible and robust to model misspecification (as they don't require any), but they may require more data to achieve comparable accuracy to model-based designs. Model-based designs can be more efficient and require less data, but they are more vulnerable to model misspecification and may be less robust in the face of complex or unknown underlying models.
The evaluation can also be different between these two DoE mindsets, with more emphasis on statistical significance with optimal designs (except for Response Surface Models and Mixture designs), vs. predictive accuracy (RMSE and other predictive performance metrics) with model agnostic designs (you're trying to have the best predictions in your experimental space, not find a significant factor or terms in a model).
Please find below a slide from presentation that I give on this specific topic, I hope it will help you make it easy/accessible for students :
I hope this answer will help you :)
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
The issue with mixtures is the dependency on level setting across multiple factors (i.e., the factors can not be varied independently). Since there are constraints, these need to be accounted for. Space filling designs provide data to create surfaces (e.g., contour plots) to evaluate performance in the chosen design space.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
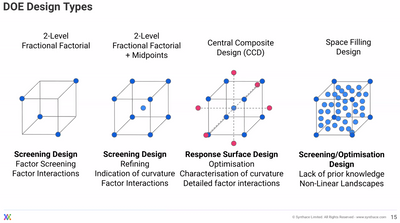
Completely agree with you @statman, depending on the objective and information about a product/process, the two design methods can be used sequentially : screen factors first with a model-based optimal approach, and then use a model-agnostic approach to optimize a predictive model in the eventuality of non-linear response.
Here is a slide from Synthace about the different designs and their possible complementarity :
There was also a paper on this topic of combining different DoE methodologies : https://community.jmp.com/t5/Discovery-Summit-Americas-2020/DOE-Gumbo-How-Hybrid-and-Augmenting-Desi...
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
Hi @frankderuyck,
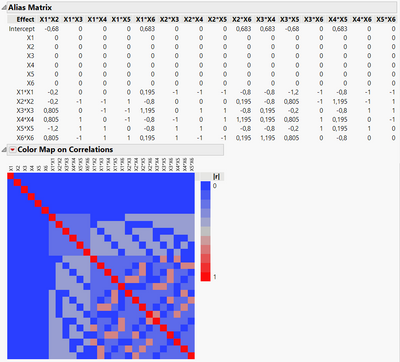
Definitive Screening Design is a "textbook" (classical) design, used for a screening case with high number of factors involved and the possibility to test interaction and quadratic effects, following the basic principles of DoE : effect sparsity, effect hierarchy and effect heredity. I wouldn't categorize this design as an "optimal" design, as the structure is "fixed" (and so are the terms screened by this design).
Concerning your conditions,
- Main effects are completely orthogonal to each other, to 2-factors interactions and to quadratic effects.
- No, there are aliases between quadratic and interaction effects :
Here is an extract from the presentation of Tom Donelly about the desirable properties of DSDs I attached earlier :
I hope this answer will help you.
You can also search for presentations about DSD from Bradley Jones in the JMP Community, he clearly demonstrates when/where to use DSDs, and the conditions to fulfill (only continuous and few 2-levels categorical factors, high number of factors, no constraint in the experimental space, easy to change factors, ...).
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
Hi @frankderuyck,
Space-filling designs and optimal designs (no matter if it is for mixture or other factors type, they can be used in both cases) are two completely different DOE mindsets: Model-based vs. Model-agnostic.
- Model-based : This type of designs of experiments involves postulating a specific model a-priori (with main effects, interactions terms, etc...), and then generating points in order to optimize the estimation of the model's coefficients. This approach assumes a specific model form and is useful when the underlying model is well-known or when there is prior knowledge about the system being studied. It may requires fewer points, and is particularly advised if you want to easily have access to explainable/interpretable results.
Example : My response Y is heavily influenced by statistically significants main effects from factor A and B, and by the statistically significant 2-factors interaction between A and B.
- Model-agnostic : This type of designs of experiments involves distributing points uniformly/homogeneously (and randomly) in the experimental space and then fitting different models to these points to obtain the best predictive model. This approach may require a high number of points depending on the complexity of the model tested (Regression, SVM, Neural Networks, Tree-based models,...), does not assume any specific model, and is useful when the underlying model is unknown or complex. But this approach may be sensitive to noise and the use of ML models may lead to overfitting situations...
Both approaches have their advantages and disadvantages. Model-agnostic designs can be more flexible and robust to model misspecification (as they don't require any), but they may require more data to achieve comparable accuracy to model-based designs. Model-based designs can be more efficient and require less data, but they are more vulnerable to model misspecification and may be less robust in the face of complex or unknown underlying models.
The evaluation can also be different between these two DoE mindsets, with more emphasis on statistical significance with optimal designs (except for Response Surface Models and Mixture designs), vs. predictive accuracy (RMSE and other predictive performance metrics) with model agnostic designs (you're trying to have the best predictions in your experimental space, not find a significant factor or terms in a model).
Please find below a slide from presentation that I give on this specific topic, I hope it will help you make it easy/accessible for students :
I hope this answer will help you :)
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
Excellent answer Victor, thanks!
I expect also another question: when use Definitive Screening instead of Optimal/Custom DOE? I don't have a straightforeward answer to this, to be honest I always use Custom.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
To come back on first question I understand that space filling is quite useful for mixtures because the underlying models can be very complex due to non-linear blending effects right?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
The issue with mixtures is the dependency on level setting across multiple factors (i.e., the factors can not be varied independently). Since there are constraints, these need to be accounted for. Space filling designs provide data to create surfaces (e.g., contour plots) to evaluate performance in the chosen design space.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
I never use always...LOL There are situations where you are trying to convince the student of the power of the experimental design methodology (vs. OFAT for example) without making it too confusing. The custom design option, while extremely flexible, can make it challenging to use. There are many options that need to be understood.
In all cases, the "best" methodology to use will likely not be known á priori. Do your due diligence, create multiple plans and evaluate the potential knowledge to be gained from each against the resources required for each. Choose with the underlying idea you will be iterating.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
Hi @frankderuyck,
Definitive Screening Design are very interesting screening designs, and they may be very useful if some conditions are met. There is an excellent blog post by @bradleyjones that gives more insights and explanations about when/where to use DSDs :
https://community.jmp.com/t5/JMP-Blog/Proper-and-improper-use-of-Definitive-Screening-Designs-DSDs/b...
And Tom Donelly did a very great Mastering in 2021 on this topic (presentation attached), with several use cases, benefits and analysis recommandetations for DSD.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
Hi Victor, is it right to state that a Definitive Screening design is a special case of an Optimal DOE where two basic conditions need to be fulfilled: (1) all main effects are orthogonal and not confounded and not confouded with other model effects (pure) and (2) no aliasing between quadratic and interaction effects. Correct?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
Hi @frankderuyck,
Definitive Screening Design is a "textbook" (classical) design, used for a screening case with high number of factors involved and the possibility to test interaction and quadratic effects, following the basic principles of DoE : effect sparsity, effect hierarchy and effect heredity. I wouldn't categorize this design as an "optimal" design, as the structure is "fixed" (and so are the terms screened by this design).
Concerning your conditions,
- Main effects are completely orthogonal to each other, to 2-factors interactions and to quadratic effects.
- No, there are aliases between quadratic and interaction effects :
Here is an extract from the presentation of Tom Donelly about the desirable properties of DSDs I attached earlier :
I hope this answer will help you.
You can also search for presentations about DSD from Bradley Jones in the JMP Community, he clearly demonstrates when/where to use DSDs, and the conditions to fulfill (only continuous and few 2-levels categorical factors, high number of factors, no constraint in the experimental space, easy to change factors, ...).
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Space filling versus optimal DOE
Thanks Victor, this is clear. Interesting discussion on community with Bradley Jones!
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us