- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Singularity problems
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Singularity problems
Hi All,
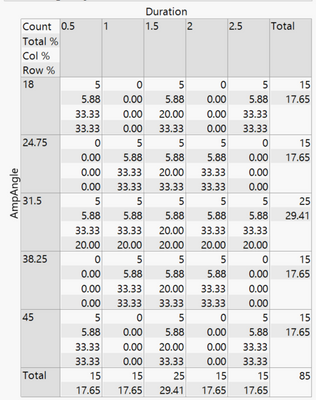
I am trying to do an ANOVA with three fixed effects. I have a fish robot and am testing the performance of three different body shapes across a range of input parameters, 5 levels of input angle and 5 of input duration. I have constructed a standard leas squares model with Shape, input angle, input duration and the full factorial of effects. I am fitting separate models to two different continuous variables measuring error. I want to see if the different robot shapes have more or less error and if they are more effected at certain combinations of input variables. When I run the model I get a bunch of singularities and the model has "lost degree of freedom" errors. The only thing I can think that could cause the problem is that I don't have a full input combination matrix. If you are looking at a 5X5 grid, I have tests for the diagonals and the cross (i.e. third level input duration X all levels of input angle and vice versa) so I am missing some crosses around the edges of the grid (this was on purpose). There is no mismatch between the treatments, I have all the trials I intended to collect.
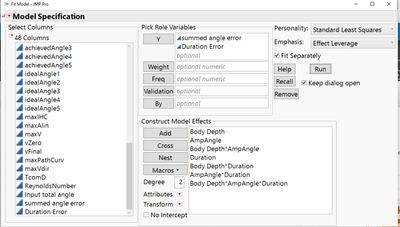
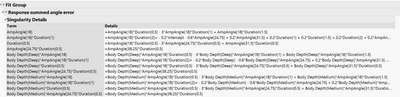
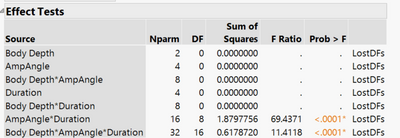
Can anyone explain why I'm getting this error and how I might fix it? I imagine I may not be doing the right test. If I coded the input angle and durations as continuous variables instead of categorical and ran a linear model instead would that give me qualitatively the same results and be valid? I've attached some screen grabs at the bottom.
Thanks,
Stephen
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Singularity problems
Do not worry about the statistics. I am not trying to turn you into a statistician! But you are using statistics so I want you to understand the meaning and the consequences of your choices.
You are free to use any design method you want of course, including making up your own design, but the method will impact the the flexibility that you have and the optimality of the design for a given task. This approach is not 'testing.' That approach is to keep trying until you find what you are looking for, or something close enough. This approach is 'experimenting' and it is all about the model. That is to say, the sole purpose of the design is to support the estimation of the parameters in the model. So everything about the model is key. Continuous factors are more informative. Continuous terms are more informative. Continuous terms are more efficient. As I said previously, I would use a continuous factor and continuous terms in the model for their advantage. You can always predict the response at the levels that are only available to you.
If you use a continuous factor, then JMP determines the optimal levels. Not all of these levels might be available to you. In that case, use the Discrete Numeric factor instead of a Continuous factor. Now you determine the levels and JMP determines the appropriate terms. (The levels and the terms must agree.") I hope that the distinctions that I am making here make sense for you.
The randomization is very important. It is not essential, but it is very important. JMP assumes that the design is randomized. That means that the selection of the treatment (factor combinations) and the experimental unit are random. It also means that all the factor levels are reset before each run. In many cases, though, the experiment sets a factor level for the first run and keeps it at that setting for the second run. This is not randomization. If it merely for convenience, consider putting more effort into the experiment, giving up some convenience, and randomize the run. If it is for practical limitations, then you must tell JMP that this factor is 'hard to change.' That indication will tell JMP what it needs to know to both make the right design and to set up the right analysis automatically.
The number of runs is a choice in the Custom Design platform. It is not available in the classic design methods as they are based on combinatorial principles and group theory. Custom design is based on optimization. You can control the number of runs (or which runs) for Fit Model by using the Exclude row state in the data table.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Singularity problems
You are trying to fit a full factorial model with data from a fractional factorial design. You do not have sufficient data to fit such a model. Think of it this way: regression analysis creates a 'model matrix' from the 'design matrix.' The model matrix contains a column to represent every term in the linear predictor that you specify. One column (typically the first) is set to 1 to estimate the intercept (constant term independent of all predictors). Another column will be the actual levels of say, Duration, to estimate its 'main effect' or the parameter for the first order term. If this factor is categorical with 5 levels, then regression creates 4 columns in the model matrix to estimate all the parameters for the main effect. A full factorial model will have terms for every possible crossing of factors. The categorical factors in the crossing will require many columns as a result. This situation sets up the possibility that two or more columns in the model matrix are identical. That is to say, the two terms in the linear predictor are aliases for the same column in the model matrix. The effects represented by these terms are confounded in the data and may mot be estimated at the same time. You cannot have identical columns in the model matrix or it will generate a singularity when the inverse of the covariance matrix is computed for the solution (i.e, estimates of model parameters). The solution is to include more runs to the design matrix with new combinations of factor levels that will produce different columns in the model matrix.
Here are some questions and suggestions.
- Which design platform in JMP did you use? I recommend custom design as the first choice in general.
- How did you define the factors? I think that angle and duration should be continuous factors. Specify the range for each and let custom design pick the best levels for fitting the model.
- Will the design be fully randomized or will some factors not be reset before each run? That answer can be very important to the design and the analysis of your study.
- How did you specify the model? Continuous factors benefit the analysis by requiring fewer parameters. For example, 5 levels of a categorical factor require 4 parameters. If the response is linear to changes in this factor, then only 1 parameter is required (slope). Fewer parameters means fewer runs. Also, typical factor ranges usually generate a response that is modeled well by a simple, low order polynomial. The full factorial model might be over-specifying the response.
- How did you choose the number of runs?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Singularity problems
So I see what you are saying about the model construction. I do want to treat input angles and durations as categorical effects because those were the input settings that were consistent across treatments. I am running other linear models that use similar measured variables as continuous effects. I was running these ANOVA to get an idea of how much motor error was happening at each input combination.
I've tried to answer your questions as best I can. I have to admit I don't have as strong a background as I would like in statistics, and I've never worked with custom designs so I'm lost when it comes to randomizing, choosing number of runs etc. If you have any resources that can help bring me up to speed I would appreciate that. I'd rather not use your time to explain basics. The JMP documentation seems to assume that one already knows the vocabulary of experiment design and so on.
- I've been using the fit model platform, I've never used custom design before
- Input angle and input duration are categorical because those are the levels we tested at. I can see the argument that we could have tested at any level so they don't need to be categorical, but since we chose distinct levels we decided to start with categorical
- I would assume fully randomized. I'm not exactly sure which factors would not be reset or why.
- I used full factorial. I probably don't need the third order term, it doesn't mean much. But I really want to see the body shape*input settings interactions
- I don't think you can specify number of runs in the fit model environment
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Singularity problems
I only have a moment now, so let me address the modeling type. The fact is, the factors are continuous and their effect is continuous, even if you can only set a small, finite number of levels. I strongly recommend that you model them as continuous effect. You can always predict what happens at any one of those discrete levels!
More later...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Singularity problems
Do not worry about the statistics. I am not trying to turn you into a statistician! But you are using statistics so I want you to understand the meaning and the consequences of your choices.
You are free to use any design method you want of course, including making up your own design, but the method will impact the the flexibility that you have and the optimality of the design for a given task. This approach is not 'testing.' That approach is to keep trying until you find what you are looking for, or something close enough. This approach is 'experimenting' and it is all about the model. That is to say, the sole purpose of the design is to support the estimation of the parameters in the model. So everything about the model is key. Continuous factors are more informative. Continuous terms are more informative. Continuous terms are more efficient. As I said previously, I would use a continuous factor and continuous terms in the model for their advantage. You can always predict the response at the levels that are only available to you.
If you use a continuous factor, then JMP determines the optimal levels. Not all of these levels might be available to you. In that case, use the Discrete Numeric factor instead of a Continuous factor. Now you determine the levels and JMP determines the appropriate terms. (The levels and the terms must agree.") I hope that the distinctions that I am making here make sense for you.
The randomization is very important. It is not essential, but it is very important. JMP assumes that the design is randomized. That means that the selection of the treatment (factor combinations) and the experimental unit are random. It also means that all the factor levels are reset before each run. In many cases, though, the experiment sets a factor level for the first run and keeps it at that setting for the second run. This is not randomization. If it merely for convenience, consider putting more effort into the experiment, giving up some convenience, and randomize the run. If it is for practical limitations, then you must tell JMP that this factor is 'hard to change.' That indication will tell JMP what it needs to know to both make the right design and to set up the right analysis automatically.
The number of runs is a choice in the Custom Design platform. It is not available in the classic design methods as they are based on combinatorial principles and group theory. Custom design is based on optimization. You can control the number of runs (or which runs) for Fit Model by using the Exclude row state in the data table.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Singularity problems
Thanks for the clarification. I think I should be fine then using the fit model platform and using input angle and duration as continuous effects. I get results that make sense.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Singularity problems
If you need any more help in the analysis, you know where to find us!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us