- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Simplifying steps in DoE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Simplifying steps in DoE
I am doing road-map of using DoE here in our department. Here are my thoughts. Please correct me if I am wrong.
Step 1. Identify if the factors are continuous and 2-level categorical. Then use DSD because identifies main effects and second order effects. Quadratic effects are orthogonal to main effects and not completely confounded with two-factor interactions. A quadratic effect might be correlated with interaction effects. A great utilization of this is for organic synthesis since most of the factors are continuous and 2 level categorical (kind of catalyst, acids, or bases). How about if the categorical factor are 3 level, can I still use DSD?
Step 2. If the factors aren't continuous and 2-level categorical then use custom design.
I believe the standard approach in DoE is to go screening (main effects) and do augmentation to add higher order effects.
But, I want to simplify our DoE protocol here in our Lab. Mostly, we have only 6 factor or less. Can we go straight-ahead in optimization without doing screening (Main effects only) using custom design?
What are pros and cons of doing either way?
Lastly, I am confused with Categorical numeric and Discrete Numeric. Can you elaborate and give examples? Are ratings categorical? I have an equipment that can only be set to 1, 3, and 5, is this categorical or discrete numeric?
Thank you
Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simplifying steps in DoE
Hello @Alainmd02,
I think there is no perfect design for every use cases, and the difficulty is to choose and create the most relevant design for each use case. DSD is an effective screening design, but perhaps you could find acceptable (or maybe better) other solutions by using directly Custom design, with optimality criterion set on D-Optimal or Alias-Optimal. Design choice is also depending on the number and type of factors you have : if number of factors > 5 and you have 1 or 2 categorical factor(s) maximum, then DSD may be interesting to consider. Below 5 factors or with more than 2 categorical factors, Custom design may be the way to go.
For your questions :
-> DSD is only able to deal with 2-levels categorical factors, no 3-levels categorical factor is allowed.
-> Augmenting may be the smart way to do, because you'll augment on significant factors only. If you try to do everything at once, it is likely that you'll end up with more experiments to do (as you expect to build a complete model with main effects, interactions and perhaps quadratic effects) compared to the augmentation method. If the difference in terms of number of experiments is not so high, maybe this is a small price to pay for more simplicity. You can also consider the new OMARS design as a compromise between DSD and full RSM designs maybe ?
-> For a good explanation about type of factors, the STIPS course about DoE may help you.
Very briefly, when you have categorical factors, your goal is to choose a level from the set of options you have entered. You can't have quadratic effects for categorical factors, only main effects and interactions. For N levels in your categorical factor, you'll have N-1 coefficients to estimate for main effects. Example of categorical effect may be : Operators (operator 1, operator 2, operator 3...), chemical nature of reagent, ... Something not described by numbers.
Discrete numerics are numbers, the only constraint is that you can't have any value between two numbers. In you case, with your equipment that can be set to 1, 3 or 5, you can choose any of these three values, but not 2,244434 for example. Same example for furnace temperature where you'll have some discrete numeric values, you can set the temperature to 180, 200 or 220°C, but not to 195 or 210°C. For discrete numeric factors, you can estimate main effects, interactions, quadratic effects... same as for continuous numeric factors.
Depending on the "nature" of rating, they can be seen as various types of responses :
- For student and teachers, notes are more likely to be a continuous response,
- If the rating is like a cotation (1: very good, 2: good, 3: average/neutral, 4: bad, 5: very bad) then it is discrete numeric (ordinal numeric),
- If the rating is like A, B, C, ... then the response is categorical.
I think in JMP 17 a new module will be very helpful for your colleagues : it's called "Easy DoE", and types of factors, settings to consider... are explained in a step-by-step approach until your final design construction.
I hope this answer will help you ! :)
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simplifying steps in DoE
I understand what you are trying to do, but you have likely over-simplified the process for proper selection (selecting of the most effective and efficient design to answer your questions). There are many things to take into account in selecting the proper tool to use. What I stress is developing a set of situation diagnostics to guide in tool selection. Without an understanding of the situation, you are likely to have a poorly designed experiment. An analogy: Your DOE strategy is to use DSD is a hammer, however you want to make a cut. There is no one strategy that will be appropriate for every situation.
Here is an abbreviated list of criteria to help in selecting the appropriate design:
- Constraints: Time, money, material availability, measurement/equipment capability, etc. How many treatments can be made (this will likely need to be negotiated)?
- How many factors are to be manipulated (the number of hypotheses to be compared)?
- How will noise be managed or partitioned (Repeats, RCBD, BIB, Split-plots, covariates...)?
- Are some factors harder to change than others? Are there other restrictions on randomization?
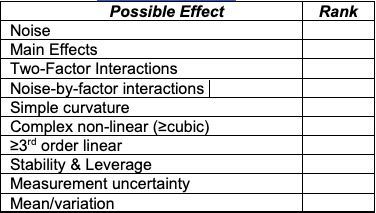
- What are the prioritized effects (see below) you want to estimate?
- Are higher order effects suspected/predicted (e.g., interactions, curvature)?
- What is the desired resolution? (What effects do you want to estimate/separate?)
- What order polynomial is necessary?
IMHO, the type of factor has less to do with experiment selection and more to do with how the experiment should be analyzed (what model or analysis platform)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simplifying steps in DoE
I want to clarify the following:
1st. I said I will use DSD if the factors are continuous and 2-level categorical. However, this tool is not appropriate if there are any linear inequality constraints on the factors or disallowed combinations of factor levels. I did not say it is appropriate for every situation.
DSD will answer your point number 1 (constraints). Time, Money, and material availability because it is more efficient than other designs. Use DSD if it fits the situation.
2nd. If any criteria does not match the DSD. Then I think the all-purpose Custom design works best.
In screening phase, do you recommend adding two-factor interaction or main effects is already enough?
or Main effects only and make alias optimal? What is the best way to do it given I have all the time, money and etc?
Given the time, money and etc. Do you always recommend Repeats, RCBD, BIB?
Split-plots are use for hard to change factors.
Actually, I do not fully understand covariate factors, when to use it.
How do I know that I eliminate noise?
3rd After screening phase. Since I know already the factors that are significant. I can use Augment Design to add higher order effects like 2-factor interaction and/or quadratic for process factors and 3-order effects (3-factor interaction and cubic) for mixture/formulation.
If I know already the significant factors. I can skip the screening phase and will go straight-ahead adding 2-factor interaction, quadratic effects for process factors and 3rd-order effects for mixture/formulation.
Please enlighten me about leverage/stability, measurement uncertainty, and mean/variation?
Thank you very much :)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simplifying steps in DoE
I'm not in a position to argue with you via this forum.
I believe you should always have a strategy to handle noise. Holding it constant is a terrible idea as it narrows the inference space. The dilemma is always how to increase the inference space without negatively affecting the precision of the design. These strategies include the ones I listed. If you do not understand them, you should seek to learn about them. Split-plots have many uses (hard to change factors is only one of those purposes). I recommend you read "Split-plot designs for robust product experimentation" by Box and Jones.
I would suggest mixture designs for formulations (not augmented designs).
If you have >15 factors, you might want to get an idea of which components to further study. You can do this with nested and systematic sampling plans to determine this leverage.
If you don't understand measurement variability, you should do this before experimentation (or nest this component within treatment) .
If your problem is one of variation (instead of the mean), then you need to get an estimate of variability for each treatment. This can be accomplished by collecting multiple "data points" (repeated measures). For example if you have within part or within batch variability, you need multiple measures of the within part or within batch and then use a summary statistic to estimate the variation. This statistic becomes one of the response variables to model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simplifying steps in DoE
I will add to @statman that this subject is deep and well-covered by textbooks and courses, from which you might glean ideas for a way to tell investigators in your area how to proceed. Stat books often get a 'bad rap' but books about DOE are quite good (well-written, understandable, practical, actionable, et cetera). If you are interested in learning more this way, let us know. We can suggest books based on your needs.
There is also training about DOE offered by JMP and it uses JMP so you get the principles and the practical skills. In fact, there will be a class in two weeks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simplifying steps in DoE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Simplifying steps in DoE
Hello @Alainmd02,
You're welcome !
I only answered about DSD and their possible use, but from what I read the topic seems a lot broader than just the use of DSD.
Reading the responses of @statman and @Mark_Bailey, I can only emphasize what they wrote : before choosing a design, there are a lot of steps to do : reflexion about the factors to change (number of factors, type, number of levels, easy/hard to change, ...), effects to be analyzed (main effects, interactions, non-linear effects, ... ?), the possible sources of noise (random variability, day-to-day variability, calibration and/or batch/run variability ....), responses precision and variance, and how related to these inputs are your goal (only screening significant effect ? Predicting values ?) and expected precision (how precise your predictions need to be compared to your measurement precision for example).
There is no perfect design for every situations.
- About mixture/formulation : If you're dealing with mixture factors (for example, ingredients in a formulation/recipe that adds up to 100% or a fixed value), you have to set up these factors as mixture factors, and this will influence the type of design you'll get (since the factors will be linked by a constraint like sum = 100% or a fixed value) :
-> mixture designs (Scheffé cubic/simplex centroïd, simplex lattice, extrême vertices, space filling, ...)
-> or mixed models (if you also have other factors that are not mixture factors).
- About the effectiveness of DSDs: As I said before, DSDs are great but they may not be the best compromise in every situation. Depending on which effects you want to see/detect, the factors you have (number and types) and the precision of your measurements, it may be wiser to do a D-optimal design with replicates instead of a DSD, to have a better estimate of response variance in your experimental space for the same number of experiments (or lower) than your DSD.
- About covariate factor, it's a variable that affects the response, but you can't control it like the other factors : you know the values of this factor in advance or you have a set of possible values, and you have to choose in this set of predetermined or possible values.
You can have more infos here : Developer Tutorial - Handling Covariates Effectively when Designing Experiments - JMP User Community
Also stay tuned and check release of JMP 17, there should be the "Easy DOE" menu that can help you and your colleagues design your DoEs :)
Hope this will help in your reflexion,
Victor
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us