- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Request for advice: Sampling validity and aggregation into distributions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Request for advice: Sampling validity and aggregation into distributions
In our lab, we measure particle sizes (specifically metal particles from single atoms up to ~20nm supported on carbon and oxide powders by STEM for anyone familliar) by aggregating data from various samples at different magnifications, similar to using Google Maps screenshots at different zoom levels to measure building sizes across the US. This approach has two main issues: the selection of sample locations and the zoom levels used.
Typically, we create an empirical distribution by aggrigating the measurements and assume the mean as the population mean. However, I'm concerned that our sampling may not be representative.
I've been using the one-way ANOVA platform in JMP to analyze particle size as a function of image number and zoom level. I want to know if i can validly aggregate the data across images within and between magnifications. High magnifications will have lots of small particles, but miss out on big ones, while low magnifications will have an opposite effect. I think the correct procedure has to do with sampling theory, but most of the sampling theory resources I can find are for social sciences, like for political polling data. However, on the other hand, this is very similar: sampling attributes over a "geographic" area.
So can I do what we've been doing and just throw them together and call it a day, or should I confirm we have representitive sampling from at least the different magnifications? If we do that, I've run some of the tests, like Tukey's that show magnifications have different means, but then I'm not sure if I need the non-paramtric versions.
How would you test the validity of our sampling and assumptions? Am I overthinking this, and should I just take the average as we've been doing? Or should I run a series of tests (e.g. Anova, anom, welch's test, tukey, etc), and which should they be? I'd appreciate any expert advice on this matter.
And sorry that this post is a tad scattershot. I see all of the options in front of me, I just have zero experience choosing between them, and this isn't something people in my field tend to care about.
Thanks!
- Tags:
- windows
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Request for advice: Sampling validity and aggregation into distributions
Here are my initial thoughts. My first question is what is the purpose for measuring particle size? What questions are you trying to answer by taking those measurements? Are you interested in reducing the variation of particle sizes for a particular product? For example, if you are trying to determine what factors affect particle size, then you might want to estimate the mean AND variation of particle sizes. You might want to estimate both within image and between image components of variation (as well as measurement error) as the factors affecting these components may be different. Most particle size analyzers (e.g., laser diffraction) I have worked with provide a distribution of particle sizes (often the distribution is not normal). My advice is to always plot the data before doing any statistical tests.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Request for advice: Sampling validity and aggregation into distributions
Thanks for the reply @statman!
@statman wrote:My first question is what is the purpose for measuring particle size? What questions are you trying to answer by taking those measurements?
So for this round of experiments, unfortunately we don't have the funds to afford this being our workhorse analysis method. So this will be used to confirm particle size measurements from another technique that will be plugged into a DoE. Assuming I can trust the sample distributions are representative of the population distribution, I then would like to do a few things.
- Pull out the first few moments of the distribution: number weighted, surface weighted (Sauter), and volume (De Brouckere) weighted average diameters.
- Compare the distributions between samples. One sample is a control that I would like to compare the others to. We have different process conditions that we could at least get a little data from a paired test on whether those conditions change the mean or variance of the distribution
Are you interested in reducing the variation of particle sizes for a particular product?
Absolutely. We've found that certain conditions narrow the distribution, which is highly desirable.
Most particle size analyzers (e.g., laser diffraction) I have worked with provide a distribution of particle sizes (often the distribution is not normal).
Unfortunately with STEM this is impossible with the scale we are working with. With biological samples, the contrast is great and automatic filters can do this sort of thing. However, we are close to the lower LOD for our instrument and it requires manual drawing of circles (ROIs) for hundreds or thousands of particles, which is a huge time sink.
You might want to estimate both within image and between image components of variation (as well as measurement error) as the factors affecting these components may be different.
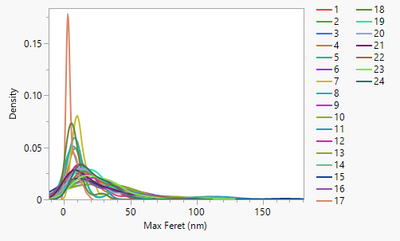
So I guess this gets to the heart of what I am wanting to do. I think I can compare samples means and variances once I've confirmed we've sampled correctly. But as you said, I need to do the within and between image analysis. However, I'm not sure how to do that. For example, here is a compare densities plot of 24 processed images from one of my samples.
As can be seen, while they all have something of the same shape, the parameters for whatever distribution model would fit all of those density curves is are going to be very different between images, because the zoomed in images disproportionately sample small particles, and the zoomed out ones disproportionately sample large particles. However..... That may be fine. We certainly need to sample all of the particle size classes, and only the most ideally dispersed sample would have the same distribution on every image. But how do I know I've correctly sampled all of them correctly? Is there a statistical test for that that involves/is weighted by sample size? Do I need to learn about bootstrapping methods to just wipe the sampling issue under the rug? These are really the points of my confusion.
Am I making sense? If not, please let me know. Thanks so much for your advice.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Request for advice: Sampling validity and aggregation into distributions
Unfortunately, I do not understand the specific situation you are in, (e.g., What is the product you are measuring? Is this a batch process? DOE on what?) If your main goal is to correlate your "typical" measurement system with STEM, then I'm not sure how "representative" the sample needs to be. Perhaps use random samples and measure those with both measurement systems? Or do you want nato ensure the extreme particle sizes measures from the 2 measurement systems correlate?
Here is some general guidance for obtaining a representative sample. There are 2 different approaches to determine how to get a representative sample (of course, you need to consider representative of what?):
Enumerative: This is an approach biased to the use of statistical method as a basis for obtaining a representative sample. The sampling is not based on subject matter knowledge. In general, guidance is to randomly sample (to reduce bias) and increase sample size. IMHO, these methods are less effective/efficient at acquiring a representative sample and since the samples are randomly acquired, assigning sources of variation to these samples is challenging if not impossible (see Shewhart).
Analytical: With this approach, the sampling is done with SME hypothesis as a basis for determining how to sample. Your scientific explanations as to why there would be variation and what factors might affect that variation are used as a basis to determine how to collect the sample and how to measure those samples. For example, Given the hypothesis that agitation speed in the processing of the materials affects particle size variation, you will need to ensure that samples are gathered from multiple speeds during processing (this may be done via directed sampling based on knowledge of the process or by experimentation). Another example, you hypothesize that part of sample preparation process (suspending the sample in a solvent) depends on the purity of the solvent so when the suspended sample dries, there are contaminants in the sample. You will need to sample over varying solvent purities. Again this may be done with directed sampling (based on knowledge of the inherent variation in solvent purities) or specifically manipulated in an experiment.
The more you understand the process, the better suited (efficiency and effectiveness) you are to develop a representative sample based on rational hypotheses. The less you understand, the more likely an enumerative approach would be useful.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Request for advice: Sampling validity and aggregation into distributions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Request for advice: Sampling validity and aggregation into distributions
Let me first suggest a different thought process with an example. Assume the changes in ambient conditions day-to-day are significant. Which is the "better" sample size? 10000 samples taken from one day, or 5 samples, one sample taken per day for 5 days. You see it is not the size of the sample that matters, it is what sources of variation are represented by how the sample was gotten.
Here are some thoughts on things you could try (again, I don't know your process well enough):
Take a sample from the "batch". Split the sample and prepare each split separately (dissolve in solvent and dry). Process one split through the STEM measurement system (I imagine this is take an image of the split). Repeat using the same split (so you now have 2 images of the same split). Measure the images at low res and collect all of the data (e.g., diameter, length, width, weight, etc.). Repeat for high res. Repeat this entire process for the second split. This will allow you to estimate the following components of variation:
1. Measurement system precision repeatability (image-to-image within split confounded with within image)
2. Split-to-split (sample preparation process within sample)
3. Res-to Res variation
Or you could correlate the high res with the low res (treat as 2 different Y's) or combine all of the data into one distribution?
You can, of course, design multiple sampling plans each differing in complexity, resources need, which components of variation are confounded, which are estimable and which are not in the study (inference space).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Request for advice: Sampling validity and aggregation into distributions
Unfortunately, we've already gotten some images so we need to analyze those. I think your comment about "...combine[ing] all of the data into one distribution" is what we are limited to right now.
Do you know if JMP has a built in way to do a weighted distribution? Like weighting differently from different levels of a factor (in this case magnification)? I think the technical term is mixture distribution or something. I couldn't find anything, but I may have missed it.
Thanks!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us