- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Replicated runs for accounting the variance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Replicated runs for accounting the variance
Hi ,
I had a custom design with 6 runs for having a model to predict the effect of temp and speed on performance . I had 5 samples each from each run. But after having the results I understood that there is lot of variance within the performance of each sample. Iwant to account include this variance in my model. I replicated each run 5 times and made a design of 30 runs. So I treated each samples performance as one run. So i believe this design would help to account for the variance within the runs.
Is this a right method? Can someone suggest alternative methods to account for those variance within the predictive model?
@Phil_Kay Coud you please take a look at this problem? Please let me know if you need more clarification in the question.
Thanks
Jerry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
Thanks, Jerry ( @Mathej01 )
It is always helpful to know as much as possible about how the experiment was done.
In this case I think the best analysis is to do as @Victor_G suggests and create a table with 6 rows (1 for each run) with Mean_Y and StdDev_Y. You can easily create this with Tables > Summary in JMP. Then analyse these as 2 responses. You can then see how the speed and temperature affect Y and also how they affect the variation in Y. So you can hopefully find settings to meet your target for Y and with minimum variation.
I hope this helps,
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
Hi @Mathej01,
Your explanations help a lot.
Concerning if your treatments need to be treated as repetitions or replications, it depends on what is considered to be your experimental unit : are your experimental units your 6 "big" samples, or the 30 parts of the big samples ?
- If your experimental unit is the "big sample", then your 5 measurements per sample correspond to different measurement points, and the runs should be treated as repetitions. You can enter the mean (or median, ...) of these 5 repeated measurements for each response, as well as an information on the variance of the measurement (variance, standard deviation, etc...) and use both responses' informations (mean and stddev for example) in the modeling to achieve a robust optimum.
- If you consider your experimental unit to be the "subset" parts, then you can consider your runs as replicates, and use a mixed model approach for this case of randomized restriction. The Whole plot will correspond to the "big" sample, and will help you in the analysis understand the variability from "big" sample to "big" sample as a random effect.
It could be also interesting to compare the two approaches and see how/where they differ or complement each others. I would go with the first option as it seems more appropriate for your experimental setup.
Another option (before any analysis or modeling) could be to visualize your data, and see for example some heatmaps for your responses on the 6 different parts and 5 related subsets, to better visualize and assess the measurement variance (I have done it on my design with 8 whole plots and 3/4 subplots) :
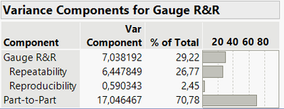
You could also use the Variability Gauge Charts (jmp.com) to better evaluate and compare your variance measurement (error) vs. signal. Use the "whole plot" (or big sample) as your "Part, Sample ID" and the subsets (repetitions) as grouping variable, and specify the response(s) you have. From this platform, you can then evaluate if your "part-to-part" signal (the differences you would like to see between your samples) is relatively high/sufficient compared to the sources of variation from your repeated measurements :
This analysis may help and complement what you can obtain with the modeling done through the Fit Model platform.
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
Hi @Mathej01,
Sorry, I'm not sure to have completely understood if your 5 runs are independant runs set at the same factors settings (replication), or if you repeat the measurement 5 times on each experimental runs (repetition). Here is some context about the differences between these two methods and which variance they account for:
- Difference between repetition and replication : Repetition is about making multiple response(s) measurements on the same experimental run (same sample), while replication is making multiple experimental runs (multiple samples) for each treatment combination.
- Replications reduce the total experimental variation (process + measurements) in order to provide an estimate for pure error and reduce the prediction error (with more accurate parameters estimates).
- Repetitions only reduce the variation from the measurement system by using the average (or other aggregated metric) of the repeated measurements.
- Use Case : In your use case, if you can measure several times (5 times) each experimental run from the design, this is a case of repetition, not replication. So it is not advised to add new rows in the datatable to bring these measurement values, as the rows/experiments added are not independent from each others (the measurements are done on one sample only, not several ones that are independent). What you can do is enter the mean (or median, ...) of these 5 repeated measurements for each response, as well as an information on the variance of the measurement (variance, standard deviation, etc...) and use both responses' informations (mean and stddev for example) in the modeling. Using these informations can help you find optimal settings for your factors, as well as increasing as much as possible the robustness of the settings (by lowering the "variance response" for each response).
If you have replicated each run 5 times, then you can do the analysis "as it is", as JMP will recognize the replications and use those runs to estimate the variability of the regression coefficients.
You should check regression assumptions, particularly homoscedasticity of errors (Residual by Predicted Plot), the linear relationship between variables and response (Residual by Predicted Plot), and the normal distribution of errors (Plot Residuals by Normal Quantiles). These plots may be helpful to determine if your experimental variance is homogeneously distributed, or if you may need other solutions, like applying a transformation to the data (before model fitting or using Box Cox tranformation in "Fit Model" platform options), or using a Generalized regression model with an adequate distribution.
More infos here on regression assumptions, diagnostics, and models evaluation/selection : https://community.jmp.com/t5/Discussions/How-I-can-I-know-if-linear-model-or-non-linear-regression-m...
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
Hi @Mathej01 ,
I agree with @Victor_G . It is important to know if these are 30 independent runs of the process. Or if there were 6 independent runs of the process with 5 measures of the outcome from each run.
E.g. how did you carry out run 2 in the table above? Did you run the process again? Or did you just re-measure the response on the outcome of run 1?
Also, if they are 30 independent runs of the process, did you carry them out in the order above? Or did you randomize so that you were changing process factors between each of the 30 runs of the experiment?
If you can let us know more about how the 30 measures from the experiment were made, then we can advise on the appropriate analysis.
Thanks,.
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
You're right @Phil_Kay, I didn't look at the run order, but the order is very important too, as it could also mean there were some randomization restrictions, implying here that factors "temp" and "Speed" would be "Hard-to-change" factors in the experimental setup.
@Mathej01 More info on the assumed model would be helpful, as well as a the datatable used for design generation, as I'm not sure about some of the levels used in the design (Speed level at 150 ?), as well as the repartition of the levels (particularly for "Speed" factor which is not completely balanced between high and low levels). If this design was intended with 2 hard-to-changes factors, the number of whole plots (or runs) may not be sufficient enough if you're interested in quadratic effects for both factors (as possibly intended with the presence of middle levels ?).
For illustration, please find attached a Custom Design with 2 hard-to-changes factors "temp" and "Speed", with 8 blocks and 30 runs, which may do a better job than the current design (if factors are hard to change and model terms include interaction and quadratic effects), available through the script "Original datatable".
Waiting for some feedback and inputs from you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
Thank you so much for your replies. I think my problem needs more explanation :).
@Victor_G Regarding the design, maximum feasible runs were 6 , and I wanted to have 150 degc and speed 200. So i treated them as discrete numeric when making the design. I assume that is fine? But i agree that the design is not very efficient.
Regarding the question of whether it's a repetition or replication, I will explain how my experiment was conducted and how the measurements were taken.
It was a coating experiment where a product was coated at different application temperatures and speeds. Only six runs were conducted, and I obtained several meters of coated samples from each run. From each of these samples, I cut out five samples and tested them for their performance under same conditions, denoted as "Y".
However, there was significant variations in the value of Y from sample to sample.This was due to unfavorable combinations of speed and temperature and which resulted in uneven dots on the coating. But i want my model to account for these variations.
According to your explanation, I believe this cannot be treated as a replication of the run?
Please correct me if I am wrong. If there is any possibility to account for these variations within my model, Please let me know.
thanks in advance
Jerry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
Thanks, Jerry ( @Mathej01 )
It is always helpful to know as much as possible about how the experiment was done.
In this case I think the best analysis is to do as @Victor_G suggests and create a table with 6 rows (1 for each run) with Mean_Y and StdDev_Y. You can easily create this with Tables > Summary in JMP. Then analyse these as 2 responses. You can then see how the speed and temperature affect Y and also how they affect the variation in Y. So you can hopefully find settings to meet your target for Y and with minimum variation.
I hope this helps,
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
Hi @Mathej01,
Your explanations help a lot.
Concerning if your treatments need to be treated as repetitions or replications, it depends on what is considered to be your experimental unit : are your experimental units your 6 "big" samples, or the 30 parts of the big samples ?
- If your experimental unit is the "big sample", then your 5 measurements per sample correspond to different measurement points, and the runs should be treated as repetitions. You can enter the mean (or median, ...) of these 5 repeated measurements for each response, as well as an information on the variance of the measurement (variance, standard deviation, etc...) and use both responses' informations (mean and stddev for example) in the modeling to achieve a robust optimum.
- If you consider your experimental unit to be the "subset" parts, then you can consider your runs as replicates, and use a mixed model approach for this case of randomized restriction. The Whole plot will correspond to the "big" sample, and will help you in the analysis understand the variability from "big" sample to "big" sample as a random effect.
It could be also interesting to compare the two approaches and see how/where they differ or complement each others. I would go with the first option as it seems more appropriate for your experimental setup.
Another option (before any analysis or modeling) could be to visualize your data, and see for example some heatmaps for your responses on the 6 different parts and 5 related subsets, to better visualize and assess the measurement variance (I have done it on my design with 8 whole plots and 3/4 subplots) :
You could also use the Variability Gauge Charts (jmp.com) to better evaluate and compare your variance measurement (error) vs. signal. Use the "whole plot" (or big sample) as your "Part, Sample ID" and the subsets (repetitions) as grouping variable, and specify the response(s) you have. From this platform, you can then evaluate if your "part-to-part" signal (the differences you would like to see between your samples) is relatively high/sufficient compared to the sources of variation from your repeated measurements :
This analysis may help and complement what you can obtain with the modeling done through the Fit Model platform.
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
Thank you so much @Victor_G ,
I choose the first option that you gave. I use both mean and standard deviation as responses.
(1) But in the prediction profiler. I am still confuse how much weightage should i give for the mean value and standard deviation. Any insight on this?
(2) And i understand the model will consider the weightage by the "importance" we give when we set the desirability. Is there a right method to choose the importance when we set the desirabilities. (figure below)
Thanks in advance
Jerry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
Hi Jerry,
You're right about the importance values, this will enable to find a trade-off between several responses, in your case between mean and standard deviation responses.
There is no rule about this tradeoff and values settings, it depends how much emphasis you want to put on the robustness of your optimum. You can try different importance values, and see if your found optimum has a standard deviation in accordance with your specifications for example : check that the optimum - 2/3 std dev is still an acceptable value for you, or try to find an higher optimum and/or lower standard deviation value.
Please note that importance can have an impact on the finding of an optimum, but also the slope of the desirability curves : the steeper the desirability curve of a response, the more influence this response will have on the finding of the optimum, as any deviation on the factors will have greater change in desirability values than for other possible responses.
I hope this complementary answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Replicated runs for accounting the variance
I agree with Phil. You have one experimental unit for each treatment. That experimental unit is "several meters of coated samples". You took 5 measures of the coated samples and measured 1 Y (performance?). Those are repeats, not replicates! You discovered that Y for the 5 samples vary significantly. The reason(s) for these variations are unknown. Consider these within treatment variation. You know they can't be because of the treatment (temp and speed) because the treatment was constant when these variations occur. So you must think about 2 things:
1. How to quantify the phenomena (variation within treatment)? Are the variations consistent within treatment? (not enough info to tell?). Are there any outliers? (perhaps graphing the data would help?) Is there any systematic pattern to the data (e.g., time series of the samples coming out from the coater?)? Will the summary statistic of standard deviation be sufficient to describe the phenomena? Are there other ways to quantify the phenomena (other Y's like coating thickness, coating viscosity)?
2. What causes the variation? Do you know the measurement system error? What x's vary during the coating process? Are the samples consistent before they get coated? There are obviously factors over and above the 2 you manipulated that contribute to variation of the coating.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us