- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Regression with a multivariate linear mixed model - Am I doing this right? and h...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Regression with a multivariate linear mixed model - Am I doing this right? and how to I extract parameter estimates and their standard errors?
I have been working on a multivariate linear mixed regression analysis in JMP and would like to check in to determine: QUESTION 1. whether or not I am on the right track?
Data collected for the analysis described below stems from a field experiment possessing a randomized complete block design, with 4 replications. The experiment has an additive design, in which crop density is elevated incrementally (200, 300, 400, and 500 plants m^-2) across two row spacings (12 and 20 cm). I am interested in evaluating how crop biomass (g m^2) is affected by the continuous variable crop density (observed values ranging from 109 to 494 plants m^-2) and the two levels of the nominal variable, row spacing (15 and 20 cm).
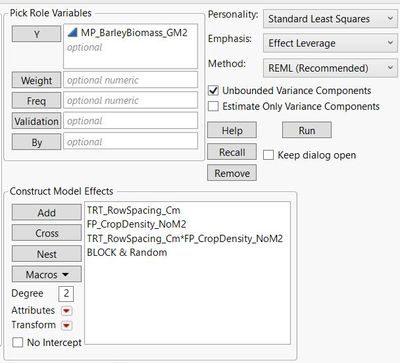
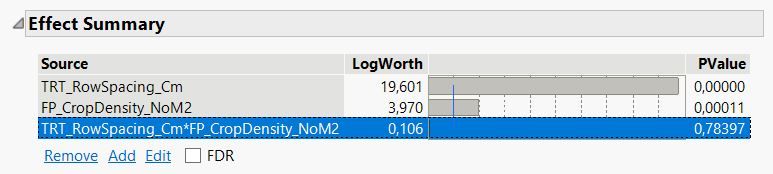
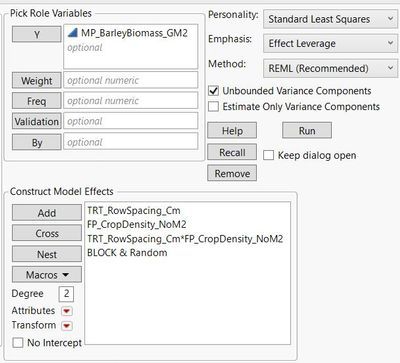
Using the fit model platform, barley biomass is evaluated as a function of row spacing (nominal) crop density (continuous), and an interaction between row spacing * crop density. Block is also included as a random effect.
Non-significant variables are removed from the model; in this case, the interaction term between row spacing * crop density was removed.
After checking the residuals by predicted plot I select dropdown > save columns > prediction forumula.
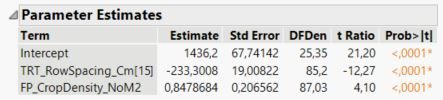
Here is what is reported in the reduced 'fit model' platform:
And when I click on the "+" symbol in the columns bar of my data table to view the 'prediction formula' saved, this is what it looks like:

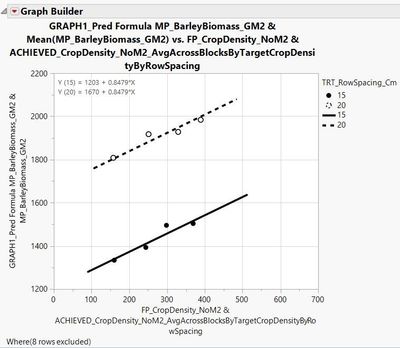
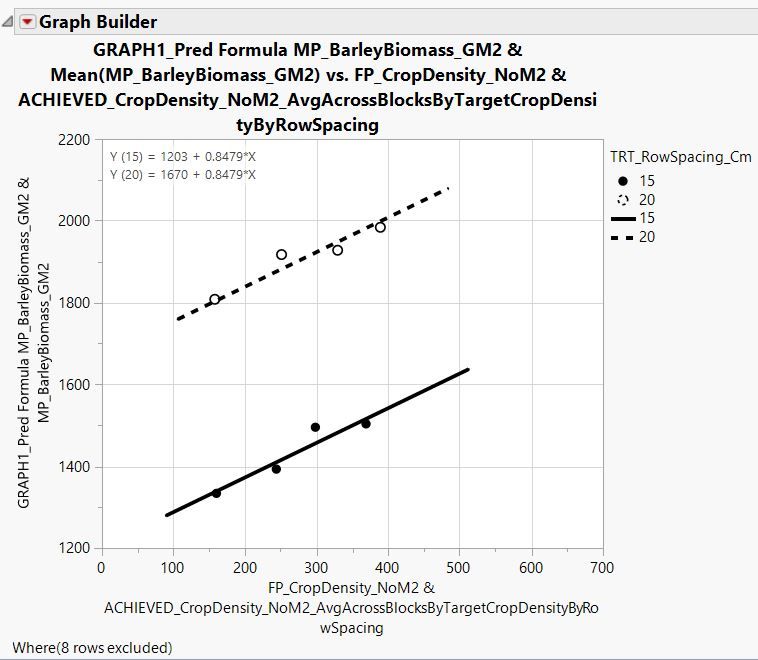
I have also made a figure in graph builder to go along with this analysis. Lines are fit to = the predicted formula on the y-axis * the continuous variable crop density on the x-axis; points are fit to the continuous variable barley biomass on the y-axis * average crop density within plots receiving the 200, 300, 400, and 500 planting densities (hence the 4X dots) across blocks by row spacing.
I would like to report in a table showing the parameter estimates and associated standard errors for the relationship between crop density (plants m-2) and all crop-biomass (g m-2), f1 (x), evaluated using the linear mixed model:
f1(x) = a(r) + b(r) * d r = 1,2
where a represents the crop biomass when crop density equals zero, b is the slope as crop density increases, d is crop density, and r1 and r2 are RS15 and RS20, respectively.
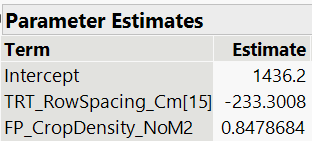
The slope, parameter b is the same for both row spacings and is 0.8479 (as seen in the predicted formula, and the parameter estimates report), and the standard error is 0.2066 (as seen in the parameter estimates report).
To calculate the intercept for the row spacing of 15 cm, parameter a(r1), I calculate 1436 - 233 = 1203 (pulling numbers from the predicted formula) and pull the standard error from the parameter estimates report, which is 19. The intercept for row spacing 20 cm, parameter a(r2), is therefore 1436 + 233 = 1669, and now I am guessing that also the standard error in this case is also 19?
Therefore, like when the 'equation' box is checked in the graph builder platform under 'line of fit' Y (15) = 1203 + 0.8479 * X and Y (20) = 1670 + 0.8479 * X.
QUESTION 2. Is this the correct way to calculate/obtain parameter estimates and their standard errors for reporting?
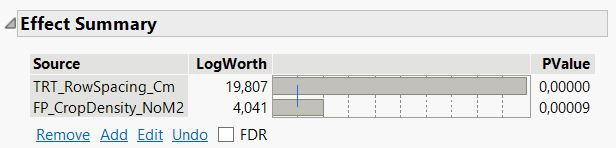
Here is a second example where the interaction term row spacing * crop density is significant and therefore keep in the model.
Here are the parameter estimates from the fit model report:
Here is the prediction formula from the saved column:
And here is the figure:
QUESTION 3. How do I go about extracting parameter estimates and standard errors in this instance?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression with a multivariate linear mixed model - Am I doing this right? and how to I extract parameter estimates and their standard errors?
It looks like you have done some good work here.
I am sorry but I find it hard to say whether you are "doing this right" just from the screenshots. It does not give me the full picture.
It can be quite complicated when you have a mixed model as you are saying that there are different components of the variation. Reporting the standard error is more complex because of this.
Are you able to attach the data table? Or an anonymised version?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression with a multivariate linear mixed model - Am I doing this right? and how to I extract parameter estimates and their standard errors?
Sure thing, and thank you for your feedback.
I have attached a 'reduced' JMP data set containing elements applicable to the two examples given in my initial post.
A quick 'tour' of items included:
- Model saved to data table titled: "CROP EFFECT ANALYSIS" is the model I used to perform multivariate mixed linear regression performed above for response variables with column titles "MP_BarleyBiomass_GM2" and "SP_BarleyBiomass_GM2".
- Additional scripts saved to the data table, titled, "GRAPH1_MP_BarleyBiomass" and "GRAPH2_SP_BarleyBiomass" will produce the figures presented in my initial post visualizing results.
- The column titled, "TRT_RowSpacing_Cm" is a nominal explanatory variable used in the model.
- "TRT_CropDensity_NoM2" is the target crop density (i.e., the treatment) prescribed to each plot, 200, 300, 400, or 500 plants m^-2, while "FP_CropDensity_NoM2" is the achieved crop density measured for each plot. FP_CropDensity_NoM2 is used as a continuous variable in the model.
- Finally, the column titled "ACHIEVED_CropDensity_NoM2_AvgAcrossBlocksByTargetCropDensityByRowSpacing" = acheived crop density (FP_CropDensity_NoM2) averaged across plots having the same target crop density (TRT_CropDensity_NoM2) and row spacing (TRT_RowSpacing_Cm) this column is used for graph building purposes.
Please let me know if you have any additional questions.
How to identify parameter estimates (especially for the SP_BarleyBiomass_GM2 example shown in my previous post) and their corresponding standard errors are my foremost question I can't quite figure out at this point.
Best wishes,
Margaret
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression with a multivariate linear mixed model - Am I doing this right? and how to I extract parameter estimates and their standard errors?
Thanks, Margaret. That really helps.
I am interested in why you have a block effect. It seems like the observations (rows) in each block are from separate plots and so they are completely independent observations of the same treatment. But you know more about the experiment than me so you probably know something I have missed.
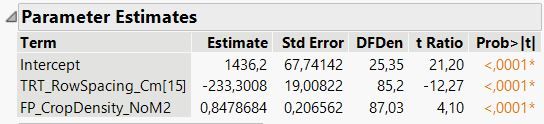
In terms of reporting the parameter estimates, you have everything you need in the parameter estimates table and I hope you can see how they relate to the Prediction Expression in JMP and the equation form that you wish to use.
However, you need to know that when you have a nominal effect with 2 levels in a model in JMP, the intercept is the prediction of the response for the average over those 2 levels. But, if you need to, you can easily calculate the intercept for each level of the nominal...
For your example the intercept is (approximately) 1436 and the effect for row spacing = 15 is -233.
The intercept for row spacing = 15 is therefore 1436 - 233 = 1203.
The intercept for row spacing = 20 is therefore 1436 + 233 = 1669.
The standard errors are the same regardless of how you define the intercept.
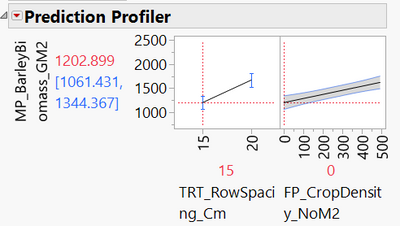
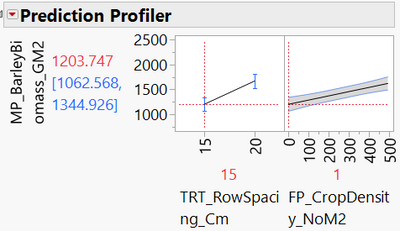
I recommend that you use the Prediction Profiler (red triangle menu at the top of the fit model report > Factor Profiling > Profiler). I think this is the best way to understand your model. You can set the variables to any value and see the response predicted by the model. For example, here you can clearly see the intercept (when crop density = 0) is 1203 with row spacing = 15:
And you can see how increasing crop density by 1 unit increases the predicted response by 0.85 units:
Similarly I think this should help you to understand how the interaction effect is parameterised.
I hope this helps.
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression with a multivariate linear mixed model - Am I doing this right? and how to I extract parameter estimates and their standard errors?
In practise, I would just report the parameter estimates as they are reported in the parameter estimates table. I would not write two formulas for the different levels of row spacing. But it is good to understand what the estimates mean.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression with a multivariate linear mixed model - Am I doing this right? and how to I extract parameter estimates and their standard errors?
Thank you very much for your responses! This is super helpful and affirming that I am succeeding in carrying out my intended analysis. The profiler is a great tool and is especially useful when understanding interactions - thank you for recommending it.
In my field, it is typical to report the parameter estimates and corresponding standard errors in a table alongside figures; therefore, my calculating them for presentation is necessary.
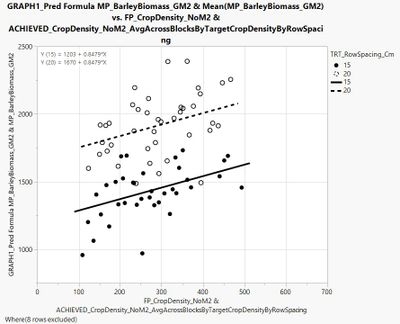
Perhaps I am missing something, but I believe that the SE of the intercept parameter should not be equal if differences are identified amongst the variable's levels. In addition, SE of the slope should differ if there is an interaction (i.e., if slope differs among row spacings tested). To refer back to the example used in your response - here is the same figure, but including all data points used to characterize the 15 and 20 cm regression lines - from this view, we can see that the SE should differ between the 15 and 20 cm line fits, since the spread of data points around each line differs. Any idea how I would go about 'extracting' the SE from the parameter estimates table?
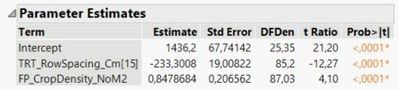
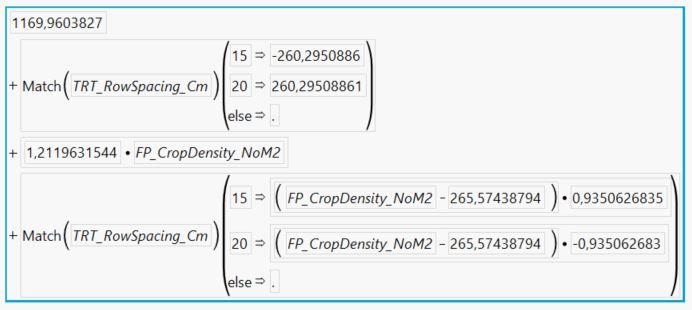
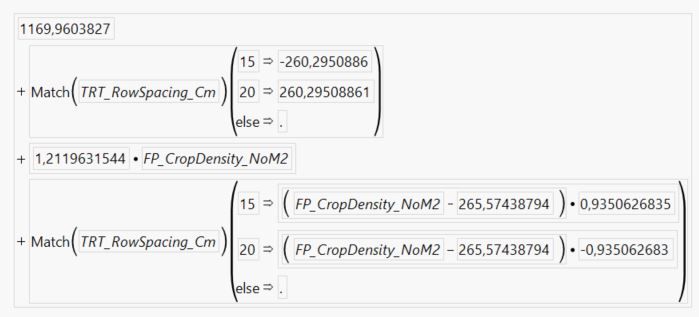
I would like to follow up by asking about how to leverage the information given in the parameter estimates table to calculate parameter estimates (and corresponding standard errors) when there is an interaction present (see SP_BarleyBiomass_GM2 example in the spreadsheet provided perviously)... For reference here is the parameter estimates table:
Here is the equation:
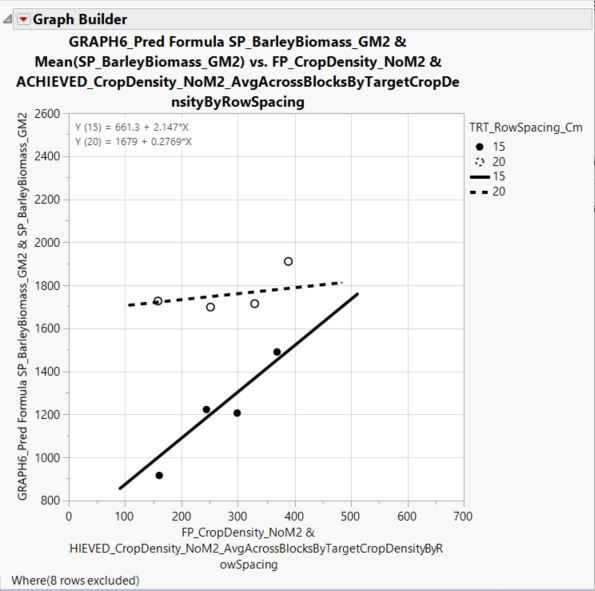
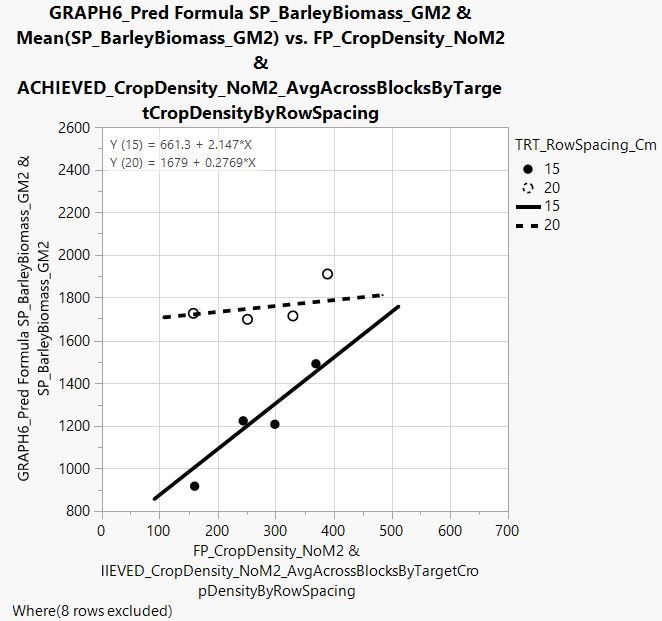
Here is the figure:
Here's my best shot - I believe that I've done it right, although I am not exactly sure why the intercepts are calculated the way that they are in this example....
- The slope of the 15 cm row spacing line is 1.2120 + 0.9351 = 2.1471
- The slope of the 20 cm row spacing line is 1.2120 - 0.9351 = 0.2769
- The intercept of the 15 cm row spacing line is 1169.96 - 260.295 + (-265.574 * 0.935063) = 661.3
- The intercept of the 20 cm row spacing line is 1169.96 + 260.295 + (-265.574 * -0.935063) = 1678.6
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Regression with a multivariate linear mixed model - Am I doing this right? and how to I extract parameter estimates and their standard errors?
To follow up on the unaddressed point in my previous post, the standard error of the intercept should differ if there is an effect of the predictive categorical variable (in this example, row spacing) and the standard error of the slope should differ if there is an interaction between the predictive continuous and categorical variables (in this example, row spacing * crop density)
EXAMPLE) MP_Barley biomass analyzed using fit model platform for mixed model analysis
STEP A) Using the fit model platform the MP_Barley biomass data set is analyzed using a multivariate linear mixed model. Model variables included the random term, block, as well as fixed terms, crop density, row spacing, and crop density*row spacing.
STEP B) The model is reduced; in this example, the interaction term, crop density*row spacing is non-significant and therefore excluded from the model.
STEP C) Formula saved and a plot is created to visualize the analysis. *Note: see previous posts in this discussion to better understand how this plot was created in graph builder.
STEP D) Calculate parameter estimates and their corresponding standard errors for reporting purposes. I learned earlier in this discussion that I can calculate the intercept for the row spacing of 15 cm (1436 - 233 = 1203) by pulling numbers from the parameter estimates report, and the intercept for row spacing 20 cm (1436 + 233 = 1669). Finally, in this case, the slope of the fit lines are equal and can be pulled directly from the parameter estimates report (0.848), and because the slope is equal across both row spacings, we can also pull the standard error (SE) directly from the report as well (0.207).
QUESTION 1: On this step, I run into trouble - How do I go about calculating the SE of the differing 15 cm and 20 cm intercept parameters?
The standard error of these two intercepts should differ since they are describing a unique sub-set of data points within the row spacing variable (15 cm and 20 cm), and therefore possess differing residual sums of squares. See example below showing that SE should differ among parameter estimates using the fit curve platform:
EXAMPLE 2) MP_Barley biomass analyzed using fit curve platform
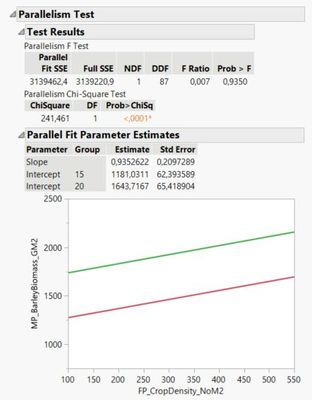
STEP A) To show what I mean by this, I've analyzed the same data set using the fit curve platform (see below).
STEP B) Select drop-down menus under Fit Curve > polynomials > fit linear
STEP C) To check whether the levels of the row spacing term (15 cm and 20 cm) share the same slope, select drop-down menu under Linear > test parallelism.
STEP D) Have a look at the parameter estimates table, and note that the SE among the intercept parameter estimates for row spacing 15 cm and 20 cm should differ.
*Note: The fit curve platform does not support mixed models, therefore the random block term is not included in the analysis; thus, parameter estimates are slightly different in the analysis below - the purpose is to show how this platform calculates the SE of each parameter, and ask, how can I produce a table containing this information on SE of parameter estimates using the output from the fit model platform that allows me to analyze a mixed model?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us