- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Recommends for Process Capability Options in JMP15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Recommends for Process Capability Options in JMP15
Hi JMP experts,
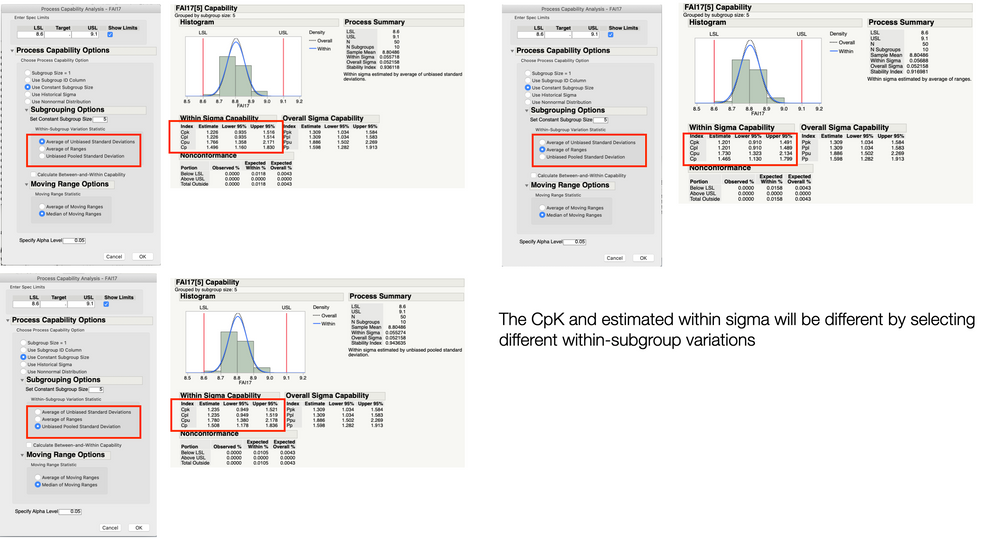
As we have multiple options selecting when doing process capability study in JMP, the process capability (CpK and the estimated sigma) will have some differences.
I know we have 'within-subgroup variation statistic' and 'moving range statistic' options.
And there are three sub-selections under 'within-subgroup variation statistic' if setting subgroup size.
I wonder to know if there is any practical guidance, recommendations in daily use. Thank you!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Recommends for Process Capability Options in JMP15
The reason why there are multiple methods in JMP for calculating what is effectively the standard deviation used in various process capability index estimates is there are varying ways in which the data has been collected and or practical considerations that need to be accounted for. These varying methods have their own unique ways of estimating the standard deviation to provide the best unbiased estimate of said quantity.
For any within subgroup variation statistic this assumes that, indeed, your data collection method supported the formation of rational subgroups. Hence you're probably using xBar/R charts to assess process stability. If rational subgroups have indeed been formed, then this is generally the preferred method.
But what about the case where the means by which the data was collected does NOT support formation of rational subgroups? The most common manifestation of this scenario is using individuals/mR charts. As such, in this case, using the moving range method is generally recommended.
All of the above methods presume a steady stable process, with no evidence of assignable cause variation for both sets of control charts, regardless of subgrouping methodology. If this presumption can't be satisfied...then calculating process capability indices is generally considered a waste of time and worse yet less than sound practice of sound quality/statistical methods. Any casual reading of anything by Deming or Wheeler in this subject matter will enlighten.
Hope this helps?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Recommends for Process Capability Options in JMP15
The reason why there are multiple methods in JMP for calculating what is effectively the standard deviation used in various process capability index estimates is there are varying ways in which the data has been collected and or practical considerations that need to be accounted for. These varying methods have their own unique ways of estimating the standard deviation to provide the best unbiased estimate of said quantity.
For any within subgroup variation statistic this assumes that, indeed, your data collection method supported the formation of rational subgroups. Hence you're probably using xBar/R charts to assess process stability. If rational subgroups have indeed been formed, then this is generally the preferred method.
But what about the case where the means by which the data was collected does NOT support formation of rational subgroups? The most common manifestation of this scenario is using individuals/mR charts. As such, in this case, using the moving range method is generally recommended.
All of the above methods presume a steady stable process, with no evidence of assignable cause variation for both sets of control charts, regardless of subgrouping methodology. If this presumption can't be satisfied...then calculating process capability indices is generally considered a waste of time and worse yet less than sound practice of sound quality/statistical methods. Any casual reading of anything by Deming or Wheeler in this subject matter will enlighten.
Hope this helps?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Recommends for Process Capability Options in JMP15
Hi Mr. Bartell,
Thanks for the advice. It helps me a lot to understand the process capability.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us