R square Adjusted for different factors

[#1]

Hello:

I have a basic question on R square Adjusted.

I ran an experiment with three continuous factors and measured the response.

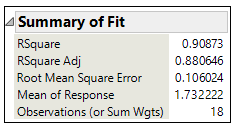
Below is the summary of Fit:

This means that I was able to capture about 88% of variability in my response.

One factor contribution was about 82% and rest was from the other factors and interaction.

Now, I realized that I missed one factor to be included in the study.

My question is:

Q1) Since I have already accounted for 88% variability, does this mean that the factor that I missed can only have a contribution of maximum 12%? 

OR

Q2) Adding of this factor in the new analysis can reduce the contribution of one factor from 82% (from previous analysis) to 60% and itself can have another 30%, because if this new factor is significant, this will vary the response as we vary this factor in DOE, this factor was kept constant in the previous run?

I am planning to run a 2^2 full factorial with one replicate and 4 CP (In total 12 runs) just for the two factors (most significant from previous run and the new factor) to practically see its implications but could not resist my curiosity.

Your help is highly appreciated.

Best Regards,

Varun katiyar

[#2 · Accepted solution]

Hi @VarunK,

You're right about the definition of R², you can describe it as an estimate of the proportion of variation in the response that can be attributed to the model rather than to random error (definition here : Summary of Fit). But R² is sensitive to the number of terms in the model : the more predictors you add (even if not useful and only random noise), the higher R² become.

In order to penalize and adjust the value of R² depending on the number of terms in the model (and facilitates models selection : comparison of models with different number of terms), you can use R² adjusted, which will take into consideration the total number of  degree of freedom you have for your dataset and the number of degree of freedom left (not used to estimate certain terms) : https://en.wikipedia.org/wiki/Coefficient_of_determination . Its value will always be less than or equal to that of R².

The closer R² and R² adjusted are, the better is your model : it means you didn't add (too many) useless predictors in your model.

In your case :

1. No, since the missing factor was kept constant in your experiments, your response variability can increase if you use this factor and change its levels. The R² adj=0,88 is only valid for your actual experimental setting, and doesn't reflect any other situation where you'll have a change of factors or factor ranges. 
2. Yes, adding a new factor in your experiments can change the repartition and ranking/importance of other factors already tested. You're adding a new dimension to your experimental space, which can have a high influence on the response variability.

I hope this will help your understanding,

[#3]

Thank you Victor.

Your help is highly appreciated.

Best regards,

Varun Katiyar