Problem with minimize function in JSL

[#1]

Hi everyone,

I am trying to use the minimize function in JSL to obtain the values of two (or more) variables that minimize the error mean square of a large model. I cannot get it to converge even though I know to which value it should converge (by trial and error). 

The basic syntax that I used is: 

minfun = Minimize( min_test, {kD( 0.4, 0.8 ), wshc( 0.1, 1.5 )}, <<Details( DisplaySteps ), <<method(sr1),<<usenumericderiv(True) );

I have tried different messages but they don't change anything.

 The goal here is to find the values of kD and wshc minimizing the expression min_test which is itself a sequence of evaluated expressions as in

min_test = Expr(
Eval( light );
Eval( parafile );
Eval( runprg );
Eval( reshandling2 );
Eval( SSE2 );
);

 The altered kD and wshc values modify the "light" and "parafile" expressions which then runs a program executable (in the runprg expression) the results of which are manipulated and from which the mean square error (MSE) is the last thing that is evaluated in the SSE2 expression. For context, the "runprg" expression submits multiple files created to a stand alone executable that simulates the thermal evolution of lakes. Each pass at the "runprg" expression requires about 10-20 seconds of computing, the results of which are reingested back in JSL to calculate the MSE.

The process itself seems to work correctly in that it reads the objective  function value correctly at each step and seems to pass the values of the parameters correctly to the expression. The problem is that the algorithm "moves" the kD and wshc parameters so slightly (only in the 5th decimal place) relative to the initial values I have given them that it fails to converge. For example, if I start with initial values of 0.8 and 0.5, respectively, I will typically obtain something like

0.8

0.49999945654133

at the next iteration and therefore is not affecting the resulting MSE significantly . With the parameters bounds I have given in the minimize function, there is plenty of space for the parameters to move. I understand that my case is pretty far from the typical simple differentiable function. However, by "manually" running the program with different parameter values, I know that the objective function is pretty convex with respect to the parameters and so thought that the minimize function would work OK , especially using the <<usenumericderiv(True) message. 

Any suggestions of a workaround that could help in this situation?

Many thanks in advance, Yves

[#2]

The algorithm will finish after MaxIter iterations - so I would bump that up to a much larger value than the default, and see if that helps.

[#3]

Thank you for the suggestion David but I'm afraid it doesn't help. However, I should have been clearer in that the number of iterations it actually does before it crashes is not high, perhaps something like 20-30, but every time the change in the parameter values is too small to have any impact.

Yves

[#4]

This is not really my area, but it seems like it should work. Here's my test JSL.

aa = expr(
	Show( "evaluating", Char( a, 19, 16 ), Char( b, 19, 16 ) ); // peek inside
	(a - 10) ^ 2 + (b - 11) ^ 2 // the function, roots at 10 and 11
);
min_test = Expr( Eval( aa ) );
a = 33; // initial guesses 
b = -55; // (not very good)
minfun = Minimize(
	min_test,
	{a( -100, 100 ), b( -100, 100 )},
	<<Details( DisplaySteps ),
	<<Method( sr1 ),
	<<usenumericderiv( True )
);
Show( minfun, a, b );

Here's the log. It seems odd that a number of calls are made with the exact same initial bad guesses, though they do seem to get a nearly perfect answer on the first *real* guess.

"evaluating";
Char(a, 19, 16) = "33.0000000000000000";
Char(b, 19, 16) = "-55.000000000000000";
"evaluating";
Char(a, 19, 16) = "33.0000000000000000";
Char(b, 19, 16) = "-55.000000000000000";
"evaluating";
Char(a, 19, 16) = "33.0000000000000000";
Char(b, 19, 16) = "-55.000000000000000";
"evaluating";
Char(a, 19, 16) = "33.0000000000000000";
Char(b, 19, 16) = "-55.000000000000000";
"evaluating";
Char(a, 19, 16) = "33.0000005066394806";
Char(b, 19, 16) = "-55.000000000000000";
"evaluating";
Char(a, 19, 16) = "32.9999994933605194";
Char(b, 19, 16) = "-55.000000000000000";
"evaluating";
Char(a, 19, 16) = "33.0000000000000000";
Char(b, 19, 16) = "-54.999999165534973";
"evaluating";
Char(a, 19, 16) = "33.0000000000000000";
Char(b, 19, 16) = "-55.000000834465027";
"evaluating";
Char(a, 19, 16) = "33.0002058854513791";
Char(b, 19, 16) = "-55.000000000000000";
"evaluating";
Char(a, 19, 16) = "32.9997941145486209";
Char(b, 19, 16) = "-55.000000000000000";
"evaluating";
Char(a, 19, 16) = "33.0000000000000000";
Char(b, 19, 16) = "-54.999660894550665";
"evaluating";
Char(a, 19, 16) = "33.0000000000000000";
Char(b, 19, 16) = "-55.000339105449335";
"evaluating";
Char(a, 19, 16) = "33.0003391054493349";
Char(b, 19, 16) = "-54.999660894550665";
"evaluating";
Char(a, 19, 16) = "32.9996608945506651";
Char(b, 19, 16) = "-54.999660894550665";
"evaluating";
Char(a, 19, 16) = "33.0003391054493349";
Char(b, 19, 16) = "-55.000339105449335";
"evaluating";
Char(a, 19, 16) = "32.9996608945506651";
Char(b, 19, 16) = "-55.000339105449335";

nParm=2  SR1      ******************************************************

Iter   nFree   Objective  RelGrad    NormGrad2  Ridge   nObj   nGrad   nHess   Parm0      Parm1      
0      2       4885       9770       9770       0       1      1       1       33         -55        

"evaluating";
Char(a, 19, 16) = "9.9999350076876112";
Char(b, 19, 16) = "11.0000734771922168";
"evaluating";
Char(a, 19, 16) = "9.9999351715994163";
Char(b, 19, 16) = "11.0000734771922168";
"evaluating";
Char(a, 19, 16) = "9.9999348437758062";
Char(b, 19, 16) = "11.0000734771922168";
"evaluating";
Char(a, 19, 16) = "9.9999350076876112";
Char(b, 19, 16) = "11.0000736560072454";
"evaluating";
Char(a, 19, 16) = "9.9999350076876112";
Char(b, 19, 16) = "11.0000732983771883";

1      2       9.623e-9   0.006344   1.925e-8   0       1      1       0       9.999935   11.00007   

"evaluating";
Char(a, 19, 16) = "9.9999999999733351";
Char(b, 19, 16) = "10.9999999999907079";
"evaluating";
Char(a, 19, 16) = "10.0000001638861082";
Char(b, 19, 16) = "10.9999999999907079";
"evaluating";
Char(a, 19, 16) = "9.9999998360605620";
Char(b, 19, 16) = "10.9999999999907079";
"evaluating";
Char(a, 19, 16) = "9.9999999999733351";
Char(b, 19, 16) = "11.0000001788046422";
"evaluating";
Char(a, 19, 16) = "9.9999999999733351";
Char(b, 19, 16) = "10.9999998211767736";

2      2       7.97e-22   2.42e-15   1.59e-21   0       1      1       0       10         11         
Convergence SUCCESS: Gradient
Time: 0

"evaluating";
Char(a, 19, 16) = "9.9999999999733351";
Char(b, 19, 16) = "10.9999999999907079";
minfun = 7.97360035815878e-22;
a = 9.99999999997334;
b = 10.9999999999907;

It looks like you might expect 27 calls to the 10-20 second function.

Does your algorithm generate the same answer for the same input, or is there a random component to it? That might make a difference.

[#5]

Very interesting Craige. I took your approach and took a peak at the values while it is running. In this example, my initial values are 0.8 and 0.5 , respectively.

minfun = Minimize( min_test, {kD( 0.4, 0.8 ), wshc( 0.1, 1.5 )}, <<Details( DisplaySteps ), <<method(sr1),<<usenumericderiv(True) );
/*:

kD = 0.8;
wshc = 0.5;
As Date(Today()) = 04Jan2024:16:39:45;
kD = 0.8;
wshc = 0.5;
As Date(Today()) = 04Jan2024:16:39:53;
kD = 0.8;
wshc = 0.5;
As Date(Today()) = 04Jan2024:16:40:00;
kD = 0.8;
wshc = 0.5;
As Date(Today()) = 04Jan2024:16:40:07;
kD = 0.80000002682209;
wshc = 0.5;
As Date(Today()) = 04Jan2024:16:40:14;
kD = 0.79999997317791;
wshc = 0.5;
As Date(Today()) = 04Jan2024:16:40:22;
kD = 0.8;
wshc = 0.500000022351742;
As Date(Today()) = 04Jan2024:16:40:29;
kD = 0.8;
wshc = 0.499999977648258;
As Date(Today()) = 04Jan2024:16:40:38;
kD = 0.800010899818014;
wshc = 0.5;
As Date(Today()) = 04Jan2024:16:40:47;
kD = 0.799989100181986;
wshc = 0.5;
As Date(Today()) = 04Jan2024:16:40:55;
kD = 0.8;
wshc = 0.500009083181679;
As Date(Today()) = 04Jan2024:16:41:02;
kD = 0.8;
wshc = 0.499990916818321;
As Date(Today()) = 04Jan2024:16:41:09;
kD = 0.800009083181679;
wshc = 0.500009083181679;
As Date(Today()) = 04Jan2024:16:41:16;
kD = 0.799990916818321;
wshc = 0.500009083181679;
As Date(Today()) = 04Jan2024:16:41:24;
kD = 0.800009083181679;
wshc = 0.499990916818321;
As Date(Today()) = 04Jan2024:16:41:32;
kD = 0.799990916818321;
wshc = 0.499990916818321;
As Date(Today()) = 04Jan2024:16:41:40;

nParm=2  SR1      ******************************************************

Iter   nFree   Objective  RelGrad    NormGrad2  Ridge   nObj   nGrad   nHess   Parm0      Parm1      
0      1       44.97207   4.89e+13   1          0       1      1       1       0.8        0.5        

kD = 0.8;
wshc = 0.500347395205604;
As Date(Today()) = 04Jan2024:16:41:47;
kD = 0.8;
wshc = 0.500308795738314;
As Date(Today()) = 04Jan2024:16:41:56;
kD = 0.8;
wshc = 0.500277916164483;
As Date(Today()) = 04Jan2024:16:42:03;

the second iteration yields this

/*:2      2       44.86266   210.178    0.080004   128     12     1       0       0.799999   0.50001    

and the 3rd

/*:3      2       45.33956   0          0.080004   4096    16     0       0       0.799999   0.50001    

and it cannot do better than iteration 2 so stops there. Here, the best objective function value is 44.86 . 

However, if I "manually" give the algorithm the parameter values of 0.52 and 1.13 (respectively), the objective function (MSE) is about 6.8, much better than the above results. The only thing I can think of is that there is a very local minimum at the initial values but that seems unlikely because I get the same kind of results no matter what my initial values are...

[#6]

I'm pretty sure minimize does depend on the slopes leading it to the answer.

In the past I've played with using a bunch of random starting points for minimize, keeping the best answer and making new random starting points with a normal distribution about that point. But that only works if you have enough time...and you never know if you've found the best answer.

[#7]

Yes, I am leaning towards a "brute force" solution similar to what you suggest. Or else, I would have to program a Nelder-Mead optimization routine which might be better suited to this kind of problems. Any chance someone at JMP have already written such a code??  

Thanks, Yves

[#8]

It's hard to say exactly what is happening without the ability to run the example myself, but there are two other approaches that come to mind that you could possibly try.  The first is to use the constrained minimize function without any linear constraints.  It uses a different method than the minimize function, so it might possibly help. So, from Craige's example you could do something like the following:

aa = expr(
	Show( "evaluating", Char( a, 19, 16 ), Char( b, 19, 16 ) ); // peek inside
	(a - 10) ^ 2 + (b - 11) ^ 2 // the function, roots at 10 and 11
);
min_test = Expr( Eval( aa ) );

minFun =
Constrained Minimize(
	min_test,
	{a( -100, 100 ), b( -100, 100 )},
	<<StartingValues( [0, 0] ), <<show details(true)
);
Eval List( {a, b, minFun} );

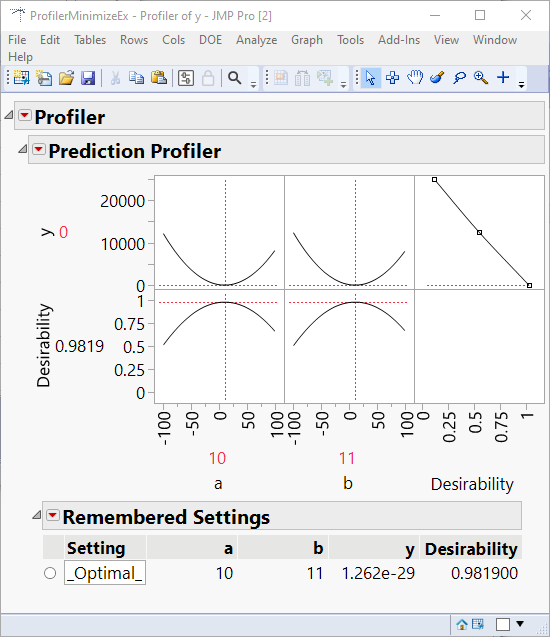
Or another approach you could try is to create a small data table and use the profiler to do the optimization.  I'm not really sure how well that will work with your formula, but I am attaching an example of how that would work with Craige's example. Here is a picture of the solution you get if you optimize the function in the profiler:

If you run the first script attached to the data table, you will launch the profiler before optimization.  The second script launches the profiler with the optimal solution. The profiler uses multiple random starts, so it is more robust for finding the global optimal solution.

[#9]

Hi Laura,

Thanks for your suggestions. So far I have only tried the first one (constrained minimize) and it sure does behave differently than the minimize function! However, now I have the reverse problem, i.e. the parameters move all over the place within the allowed parameter space without seemingly ever reaching stable values!! One thing I am not quite clear is the difference between "iterations" and the number of times the objective function is evaluated. Clearly they are not the same. I had set a max iter(5) but the function was evaluated many more times without converging. I had to force quit JMP after a few minutes. 

I am beginning to think that the type of model I am trying to optimize is rather pesky!

I'll give a shot to your second suggestion! Best regards, Yves