- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Probit Analysis & Fit Testing
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Probit Analysis & Fit Testing
I am using the Simple Probit Analysis script add-in to determine LD50, LD90, and LD95.
Is this script capable of correcting with Abbott's, or how do you set this up? Currently, I corrected the data myself by applying the Abbott's correction to the raw data to adjust for mortalities.
After running the Probit Add-In, how do I determine goodness of fit? There are no Chi Squared results. Is there another way I can run this analysis to get my LD values, as well as getting the Chi Square?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
Please see my reply with a complete analysis that ends with the question, "So we agree now, no?" It shows you how to set up your data in a JMP data table. It also shows you how to assign the data columns to the analysis roles in the Fit Model launch dialog and change the other settings for a proper Probit analysis. I did not apply any transformation to the dose levels - it is unnecessary.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
Excluding the high responses is not acceptable from a modeling or statistics point of view. You are suggesting that you exclude valid data to overcome a basic flaw with the study. (I understand that you could not foresee the potency of this agent, but that does not remove the flaw in the data.) You need more data, between dose = 0 and dose = 1.64, not less data, to solve this problem.
Excluding the high dose samples might be acceptable in your situation but I could not justify it. The fact that you (possibly) obtain a 'better' model this way is not validation. You simply cannot determine the LD50 from this sample of dose-response data except to say that LD50 occurs between 0 and 1.64.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
Did you contact the author of the add-in or read the description and instructions first?
JMP has several built-in platforms that can estimate such quantities and provide goodness of fit statistics. These leads should get you started.
- Fit Curve can fit common non-linear functions.
- Nonlinear is more general and it can fit custom models.
- Generalized Linear Models can perform a probit analysis.
Did you search probit yet in Help or Help > Books > Fitting Linear Models?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
I have not.
I have been attempting to run the model in the Generalized Linear with Probit, however, my LD values do not match up with what the Probit Add-In is giving me, so I'm not sure what is going on. I've read through the Fitting Linear models, but what I am trying to run analysis on is nonlinear, which I honestly don't have any experience with in JMP.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
This example is from our training course, JMP Software: Analyzing Discrete Responses.
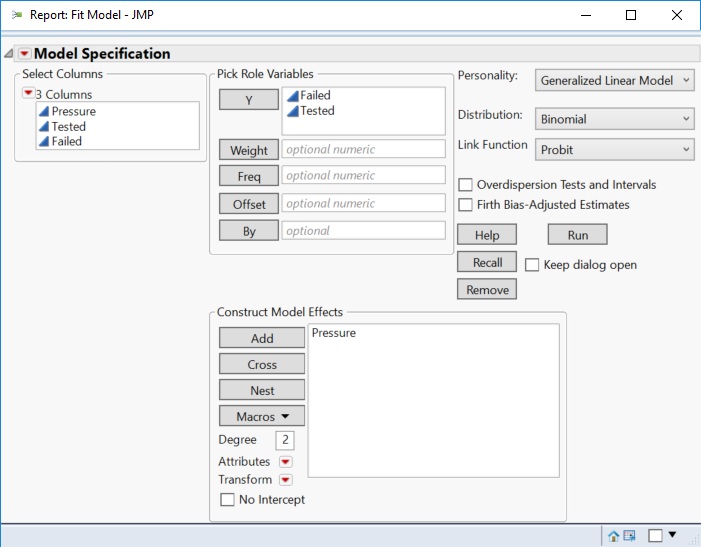
We are testing seals for failures at increasing pressure levels. Here is the data table with the preferred layout:
Note that we do not enter the failure rate (Failed / Tested) for the response.
Select Analyze > Fit Model. Select Pressure and click Add. Select Failed and click Y. Select Total and click Y. (Note that (1) you must enter a column with the count of targets and another column with the count of opportunities and (2) the must be entered exactly in that order.) Click Standard Least Squares and select Generalized Linear Model. Select Binomial for the Distribution model. Select Probit for the Link function. Your launch dialog should look like:
Click Run.
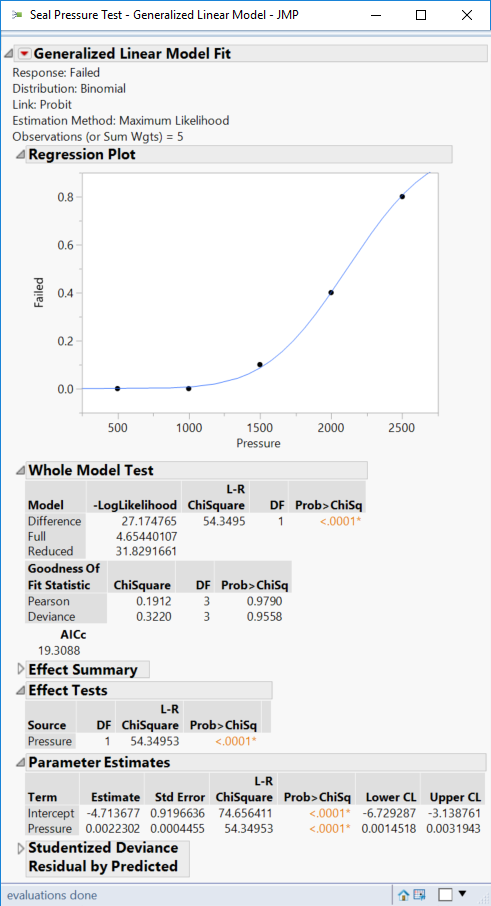
You can see the non-linear response and the regression diagnostics below:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
Okay,
It seems if I include my 0s (Control for Mortality) into the model, both the general linear probit model and the probit add-in match up the LD recommendations. If I use Abbott corrected data, then they have discrepancy between the two.
Should I run the model with the 0s and the raw data (no Abbott's adjustment), or is it more correct to adjust the raw data with Abbott's prior to inputing into the probit and disclude the 0s?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
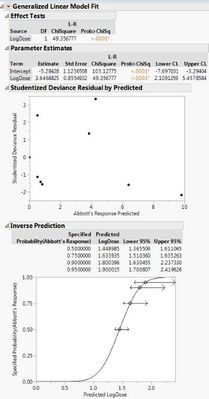
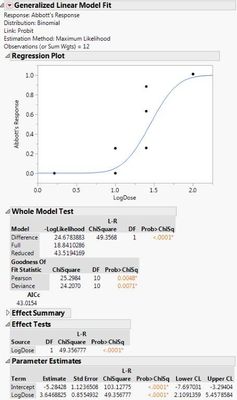
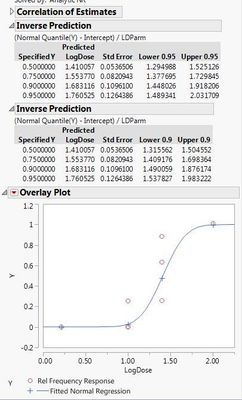
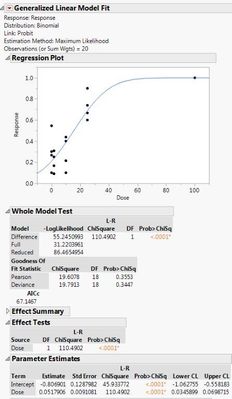
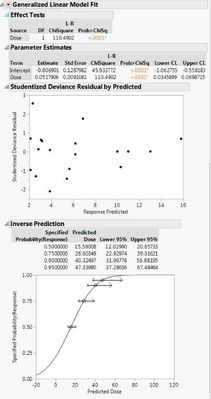
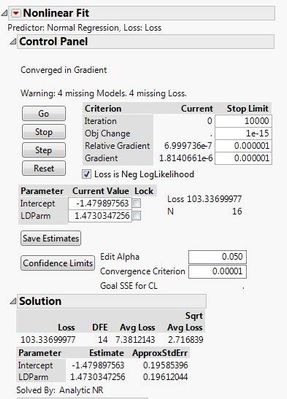
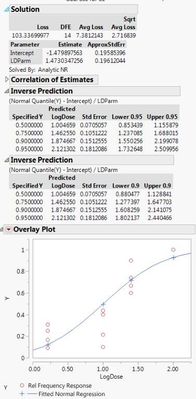
Here are the two different results I'm getting with the different data sets. If I use the 0s and my raw data, both the probit model and the general linear probit model seem to match up. However, if I correct my data with Abbott's correction and leave out the 0s, then the two models don't match up.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
I attached the wrong Linear models with raw data. Here are the correct: 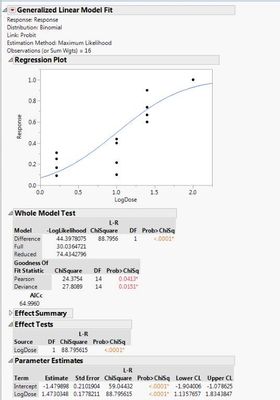
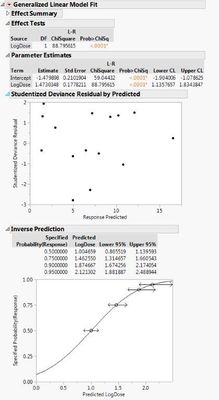
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
Abbott's correction is applied to mortality rates (i.e., proportions) to account for the natural mortality in the absence of the agent be tested. GLM is modeling a binomial distribution with a linear predictor. The GLM model has an intercept for that purpose (baseline mortality). So it is not necessary to apply this correction and doing so will, in fact, change the output. So don't do it if you are using GLM for your analysis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
So if I use the GLM analysis, do I include my 0s/Control Data and my initial raw data? And in doing so, is it correct to adjust a "0" to "0.005" for the log transformation? I am testing for mortality rates in the presence of an agent at various time points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Probit Analysis & Fit Testing
I am confused as much as you are.
You should have two counts for your response for each level of the predictor: one count is the number that died and the other count is the number that might have died. You should have one predictor. It is usually concentration or log concentration. Is that true? Or is it time? Are you trying to estimate the time for LD50 at a fixed concentration?
Please use the data format exhibited in the example that I shared and not rates or proportions. Counts are necessary for the inference. A rate of 0.1 might result from a case of 1/10 or a case of 100/1000. The rate is the same in both cases but the sample size is very different.
Once again, if you enter the data as I showed and set up the GLM as I showed, you can forget about Abbott's correction for rates. You should enter both counts for time=0.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us