Discussions
Solve problems, and share tips and tricks with other JMP users.
Accepted Solutions
Hi @Mariana_Aguilar,
I see at least 2 options to explore your curve dataset (one with JMP, the second one with JMP Pro) :
- With JMP : You could use the platform Fit Curve with a stacked data format, setting "Intensity normalized" as Y, "Wavelength (nm)" as X and "Sample" as By variables. Then, you can fit a Skew Normal Peak (available in Peak models in the red triangle) to your 4 samples, and extract the fitted curves parameters : Location, Scale, Skew and Peak value (right-click on table "Parameter Estimates" and click on "Make combined datatable"). A new table will open in a stack format.
You can split this table and use the parameter estimates in the PCA platform, to assess how similar/different are the two processes and composition :
Most of the variation seems to come from the process, with the first principal component responsible for approximately 95% of the variation in parameters values and linked to process.
Hierarchical clustering would also show you that the biggest difference between samples could be linked to a difference in process (pasteurization vs. dispersion, first split in the clustering) : -
With JMP Pro : You can use the Functional Data Explorer with a stacked data format, setting "Intensity normalized" as Y, Output, "Wavelength (nm)" as X, Input and "Sample" as ID, Function variables.
You can then fit a B-Spline model to your curve data, and a cubic model with 17 splines should work well :You can then directly look at the Score plot to visualize your samples with one or two Functional Principal components :
You'll once again see that process seems to be the biggest difference in the curve profiles of your sample (corresponding to FPC1 responsible for 99,8% of the variation in the curve data).
This process importance conclusion can also easily be visualized through Graph Builder (the two samples ID are very similar, but the change in curve can be mostly be imputed to process differences) :
Please find scripts to follow the analysis described here in the attached datatable.
I hope these two solutions may help you,
Hi @Mariana_Aguilar,
I see at least 2 options to explore your curve dataset (one with JMP, the second one with JMP Pro) :
- With JMP : You could use the platform Fit Curve with a stacked data format, setting "Intensity normalized" as Y, "Wavelength (nm)" as X and "Sample" as By variables. Then, you can fit a Skew Normal Peak (available in Peak models in the red triangle) to your 4 samples, and extract the fitted curves parameters : Location, Scale, Skew and Peak value (right-click on table "Parameter Estimates" and click on "Make combined datatable"). A new table will open in a stack format.
You can split this table and use the parameter estimates in the PCA platform, to assess how similar/different are the two processes and composition :
Most of the variation seems to come from the process, with the first principal component responsible for approximately 95% of the variation in parameters values and linked to process.
Hierarchical clustering would also show you that the biggest difference between samples could be linked to a difference in process (pasteurization vs. dispersion, first split in the clustering) : -
With JMP Pro : You can use the Functional Data Explorer with a stacked data format, setting "Intensity normalized" as Y, Output, "Wavelength (nm)" as X, Input and "Sample" as ID, Function variables.
You can then fit a B-Spline model to your curve data, and a cubic model with 17 splines should work well :You can then directly look at the Score plot to visualize your samples with one or two Functional Principal components :
You'll once again see that process seems to be the biggest difference in the curve profiles of your sample (corresponding to FPC1 responsible for 99,8% of the variation in the curve data).
This process importance conclusion can also easily be visualized through Graph Builder (the two samples ID are very similar, but the change in curve can be mostly be imputed to process differences) :
Please find scripts to follow the analysis described here in the attached datatable.
I hope these two solutions may help you,
Hi Victor, thank you for your kind and thorough answer.
I have a couple more questions if you don't mind...
1. For the first option (using the Fit Curve menu). I can't seem to find the Skew Normal Peaks under the Peak Models menu. I've tried with Gaussian (green) but at least visually it doesn't seem like a great fit. Then I tried with ExGaussian which seems better, but, I'm unsure on whether I'd be introducing more complexity onto my fitted curve parameters?
And my second question is in regards of the second option.
From the Functional Data Explorer Platform, do you know how can I save the Principal Components obtained so that I can proceed with Hierarchical clustering? (or if there's another option within the platform to move on to clustering?)
Thank you so much!
Mariana
Oh one more doubt if I may!
In the functional data explorer platform, what's the difference between doing B-Spline to pre-process the data first vs going straight to use Direct Functional PCA on the models menu (under the red triangle):
thank you!
Hi @Mariana_Aguilar,
The difference is in how the data is used and pre-processed as you mention : with a B-Spline or P-Spline, you first use a model that correspond to your raw curves data, and then you can calculate Functional Principal Components based on this model (approximation).
With direct models like direct Functional PCA, you directly perform a Singular Value Decomposition (SVD) on your raw data to extract eigenvalues and eigenfunctions. More info here : Types of Functional Model Fits
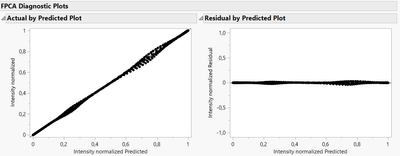
To determine what would be a suitable option, you can fit different models and evaluate them based on statistical metrics (like information criteria AICc and BIC), and with the visualizations of the Diagnostic plots to evaluate model's adequacy/precision. In your case, it seems that applying B-Splines before extracting Functional Principal components with your curves data is a good option, as the residuals from the models are very low and homogeneous, unlike those from Direct Functional PCA :
Diagnostic plots for B-Splines :
Diagnostic plots for Direct FPCA:
Hope this answer will help you,
Hi @Mariana_Aguilar,
Concerning your questions :
- I think this new model type "Skew Normal Peak" has only been introduced in JMP 18, so if you're working with JMP 17, you will only have access to the three choices you mentioned : Fit Curve Options
If you can't have JMP 18 for the moment, I agree that ExGaussian might be a more suitable modeling option, as it seems your peaks are a little skewed. The Gaussian peak model is more appropriate if you have symetrical gaussian peak.
I don't understand how ExGaussian might add more "complexity" in the model, as there will be only a difference of one parameter in the model complexity between ExGaussian and Gaussian. Looking at information criteria AICc and BIC, you can see that adding one parameter does improve the modeling, there is a better balance between model fit and model complexity (the lower the information criterion AICc/BIC, the better). - In the Functional Data Explorer platform, you can save the Functional Principal Components : go into the "Function Summaries" panel, click on the red triangle, and from there you can customize and save the function summaries and FPCs :
You can directly visualize your samples in a 2D plot with the FPCs when looking at the Score plot :
I hope these complementary answers will help you,
