- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Multiple regression with dummy variables
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Multiple regression with dummy variables
How can I select intercept in multiple regression?
I want two lines to cross the Y axis in the (0,100) point.
Thanks
Tohar
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiple regression with dummy variables
I assume that you selected Analyze > Fit Model to start the multiple regression. A check box is at the center of the bottom of the launch dialog. Select it to remove the intercept from the model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiple regression with dummy variables
This post describes how to use the Fit Y-by-X/Bivariate platform with by() .... to collect the slopes and intercepts:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiple regression with dummy variables
Perhaps more details are needed as I am the third to respond and I have a different take on your question. You said you wanted the lines to go through (0, 100). That is not the same as having the y-intercept of zero. You could use the nonlinear platform to build a model with a fixed y-intercept of 100 and the rest of the linear model to estimate the parameters with that restriction.
Provide a bit more clarity of your situation so that we can better assist you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiple regression with dummy variables
Oh, thanks, I miss-read this sentence.
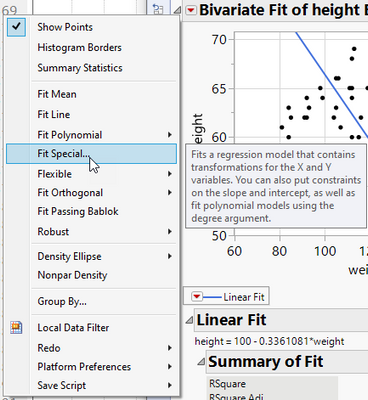
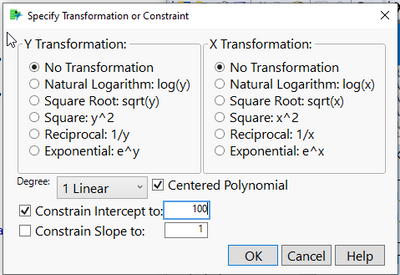
In the Fit Y - by - X / Bivariate Platform there is also an option to set the intercept to a fixed value:
Constrain intercept to
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiple regression with dummy variables
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiple regression with dummy variables
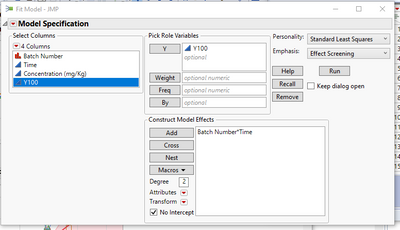
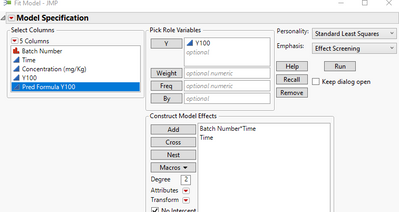
@Tohar , so it sounds like you have an ANCOVA model (one categorical factor C, and one continuous X) and you want to regress Y on these. Define Y100 = Y-100. then use Y100 as your response. then the only effect in your model will be C*X, with no intercept. See pic below. Also, in the red triangle pull down menu deselect "Center Polynomials".
Run this and get the following: And remember Y100 is Y-100. So, when Y100=0, Y=100. You can then get creative with Save Prediction Formula/Graph Builder/etc to get the Y axis back to the raw scale (shift it back up by 100).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiple regression with dummy variables
Thank you very much
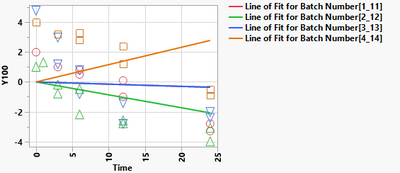
I am not about the result I got; the lines cross the Y axis in (0,0) - see attached.
My goal is to check if there is a difference in rate (ie slope) between the two treatment groups. It is not necessary to check whether there is a difference in the intercept, I want to set it both in the model and in the presentation graph at (0,100).
Many thanks!!!!!
Tohar
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiple regression with dummy variables
@Tohar Assuming your model is correct (I have my doubts from looking at your residual plots etc), the p-value for the parameter estimate and/or in the ANOVA table tells the story (they are equivalent) If less than 0.05 (that is the "usual" threshold /Type 1 error rate) then you could claim that there is a difference in slope. Strictly speaking, you are testing whether or not there is any difference from the reduced model Y100=0 (i.e, just noise). The p-value says reject the Y100= 0 model in favor of the two slope model (where slope1 = - slope2).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multiple regression with dummy variables
@Tohar . On second thought, use the same model with the interaction (as I said) and Days From Start.(see below). Then assess the equivalence of slopes via the p-value for the interaction parameter estimate. Adding the extra term will give more flexibility wrt the slope estimates (doesn't force slope1 = -slope2).
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us