- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Mean Difference with confidence intervals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Mean Difference with confidence intervals
So I'm running an experiment that tests rodents consumption of seeds. The results showed that rodents from the control group consumed 898 seeds on average whereas another group of rodents that received treated seeds consumed only 447 seeds on average. I would like to express these results as the phrase, "rodents from the treatment group consumed 50.2% less seeds than those from the control." {1-(447/898)=.502} Calculating the percent change is easy enough, but I would like to build a confidence interval around that relative percent change. Is there a simple way to calculate this or a shortcut in JMP that might display it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mean Difference with confidence intervals
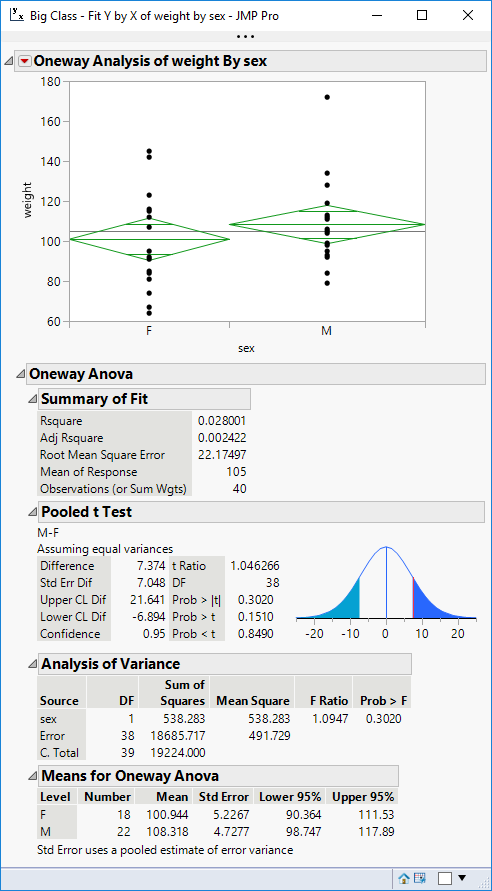
I believe from your description that this is a case of a simple two-sample t-test. Here is an example, using weight versus sex from the Big Class sample data.
The Pooled t Test outline reports the point estimate and the 95% confidence interval estimate for the difference. Can you convert these values to percentage difference?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mean Difference with confidence intervals
Sorry, I should have clarified with the initial question. I'm actually doing an ANOVA. I need to compare 6 types of treated seed to a control. Is there a way to get the difference confidence interval in the Fit Model Output. Also how would you suggest converting this difference to a percent? I'm not sure what the denominator would be.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mean Difference with confidence intervals
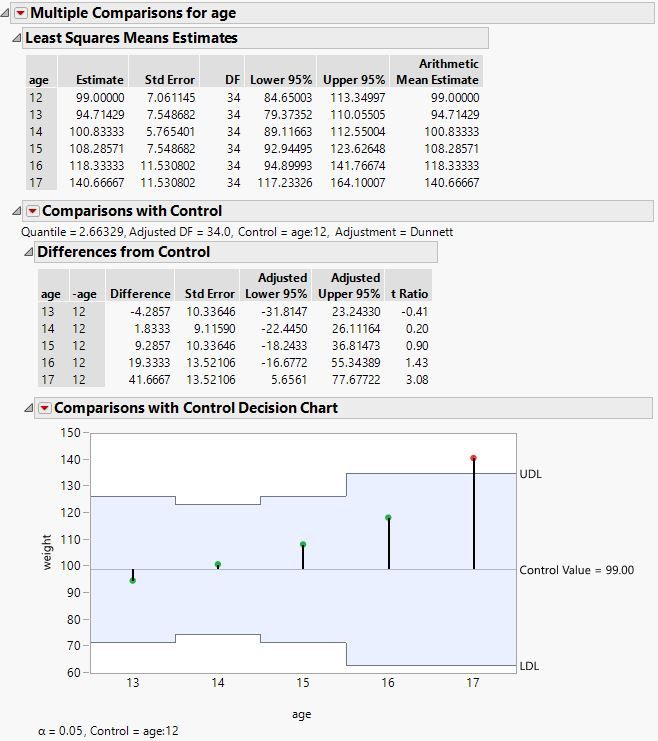
Select Analyze > Fit Model. Enter your response as Y and your predictor with Add (Effects) and click Run. Click the red triangle at the top left and select Estimates > Multiple Comparisons, select Comparisons with Control - Dunnett, and then click OK. Select your control level and click OK. You will get a table like this:
Can you use the differences here for your purpose? Note that you can right-click on the table and select Make Into Data Table. You can now use column formulas to compute values or visualize the table with Graph Builder.
I don't know how to calculate percentages.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mean Difference with confidence intervals
The phrase, "Rodents that recieved seeds treated in compound A ate 451 less seeds than those offered control seeds.(CI: 3??, 5??)," is not nearly as informative as the phrase, "Rodents that recieved seeds treated in compound A ate 50.2% less seeds than those offered control seeds.(CI: ??%, ??%),"
I could publish this phrase without a confidence interval, but I feel that it would raise questions from a statistically minded review without the interval.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us