- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Mathematical Equation to Forcecast with SARIMA Model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Mathematical Equation to Forcecast with SARIMA Model
Hi .... I am new here and need your help.
I am developing a SARIMA model
The model is predicting the following Formula:-
ARIMA Forecast(
:Actual MS,
120,
Seasonal ARIMA( 2, 1, 1, 1, 1, 3, 12 ),
{AR Coefficients( {-0.0941622870204595, -0.0767935781741432} ),
MA Coefficients( {0.550123670174196} ),
Seasonal AR Coefficients( {-0.0631251223075085} ),
Seasonal MA Coefficients(
{0.618076346003494, 0.420495338021673, -0.269501862686839}
), Seasonal Lag( 12 ), Intercept( -0.0202269450580077 )},
Row() - 120,
Row() - 120
)
How do I convert it into a mathematical equation to predict the future demand?
Regards
Ramesh
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mathematical Equation to Forcecast with SARIMA Model
The formula that you gave is not correct, by just looking at the maximum lag. If you are really into finding the truth about SARIMA formulas, I recommend that you check out the book "Time Series Analysis: Forecasting and Control", by Box, Jenkins, and Reinsel. ARIMA models are also known as Box-Jenkins models, that is why.
Now talk about (2,1,1)(1,1,1)12 model. First let me get the name right to facilitate the explanation: (p=2,d=1,q=1)(P=1,D=1,Q=1)S=12.
There are totally six polynomials: two for AR part (involving p and P), two for MA part (involving q and Q), two for differencing part (involving d and D).
Start with the differencing part, which is the product of two polynomials: (1-B)(1-B^12). This means the series is preprocess by differencing: Z[t] = Y[t] - Y[t-1] - Y[t-12] + Y[t-13].
Then the series Z[t] is modeled by an SARMA model, notice the "I" in the middle is gone.
Now look at the AR part, which is the product of two polynomials: (1 - phi1* B - phi2* B^2)(1 - phi3* B^12). Expand it I get: (1 - phi1* B - phi2* B^2 - phi3* B^12 + phi1*phi3* B^13 + phi2*phi3*B^14).
Now look at the MA part, which is the product of two polynomials: (1-theta1 * B)(1- theta2*B^12). Expand it I get: (1-theta1*B-theta2*B^12+theta1*theta2*B^13).
Now put AR polynomial and MA polynomial in the equation:
(1 - phi1* B - phi2* B^2)(1 - phi3* B^12). Expand it I get: (1 - phi1* B - phi2* B^2 - phi3* B^12 + phi1*phi3* B^13 + phi2*phi3*B^14)Z[t] = (1-theta1*B-theta2*B^12+theta1*theta2*B^13)a[t].
Now put Z[t] on the left side of the equation, and all other terms on the right:
Z[t] = (phi1* B + phi2* B^2 + phi3* B^12 - phi1*phi3* B^13 - phi2*phi3*B^14)Z[t]+ (1-theta1*B-theta2*B^12+theta1*theta2*B^13)a[t]
Now apply back operator rules, and get:
Z[t] = (phi1* Z[t-1] + phi2* Z[t-2] + phi3* Z[t-3] - phi1*phi3* Z[t-13] - phi2*phi3*Z[t-14]+ a[t]-theta1*a[t-1]-theta2*a[t-12]+theta1*theta2*a[t-13]
Notice a[t] = 0. Z is the differenced series, which you should be able to calculate from Y series using the formula that I mentioned about. the remaining a values are innovations from the fitted model. So, you should be able to get Z[t] now.
Now look at Z[t] = Y[t] - Y[t-1] - Y[t-12] + Y[t-13] again. Re-arrange it, and I get Y[t] = Z[t] + Y[t-1] + Y[t-2] - Y[t-13]. So I can get Y[t] given all previous Y's and Z[t].
The explicit formula of Y[t] is far more complicated than the formula that you provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mathematical Equation to Forcecast with SARIMA Model
Good news, the JSL you posted is the model.
Not sure how you got JMP to make it for you, but it looks a lot like a prediction formula
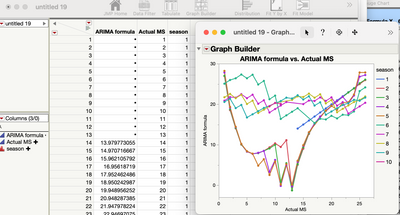
I pasted your formula into a column formula, made a second column that repeats 1-26, and gave it the name "Actual MS".
You probably have a data table with 120 rows or more and this formula along with the data you're modeling.
All you have to do is add more rows, insert some data and the prediction formula already in the table will calculate your forecasted results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mathematical Equation to Forcecast with SARIMA Model
Sir, what you have suggested works only when one has access to JMP.
I am interested in the mathematical formula which is creating the prediction. I can then use the mathematical formula to make prediction when I don't have access to JMP.
.
Regards
Ramesh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mathematical Equation to Forcecast with SARIMA Model
The SAS code to make the prediction is
// Formula Editor Publish
New Column( "ARIMA Forecast",
"Numeric",
Formula(
ARIMA Forecast(
:Actual HSD,
120,
Seasonal ARIMA( 2, 1, 1, 1, 1, 1, 12 ),
{AR Coefficients( {-0.0446867759168569, -0.00612002018236452} ),
MA Coefficients( {0.729485379327256} ),
Seasonal AR Coefficients( {0.150588923188078} ),
Seasonal MA Coefficients( {0.930743182626315} ), Seasonal Lag( 12 ),
Intercept( -3.16936375022134 )},
Row() - 120,
Row() - 120
)
)
);
I would like to know the mathematical equation that this code converts to make the prediction.
Regards
Ramesh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mathematical Equation to Forcecast with SARIMA Model
Formula Depot might work if you have access to JMP Pro?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mathematical Equation to Forcecast with SARIMA Model
The mathematical equation is very similar to the equation that describes the model; see here Statistical Details for ARIMA Models .
To make forecasts, start with one-step-ahead forecast, i.e. forecast Y[t+1], given Y[t], Y[t-1], .... and a[t], a[t-1], ..., which are the innovations obtained from the model. The value for a[t+1] is zero, because that is the "one-step-ahead" innovation, whose expectation is zero. Plug in all the known quantities, and solve the only unknown one: Y[t+1].
Then move on to the next one Y[t+2], given Y[t+1], Y[t], .... and a[t+1], a[t], ...
After the last step, you literally get the formula that you are looking for. It is a convoluted sum of known quantities.
ARIMA and SARIMA are conceptually identical, SARIMA is only a little more complicated by involving a multiplication of polynomials. But after expanding the multiplication, the procedures are same.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mathematical Equation to Forcecast with SARIMA Model
For my Time Series data, the SARIMA model that is best able to forecast is (2,1,1)x(1,1,1),12.
The mathematical formula given in literature for above SARIMA configuration is
Yt = α + β1Yt-1 + β2Yt-2 + βpYt-12 + Φ1(Yt-1 – Yt-2) + Φ2*(Yt-1- Yt-12)
The value of the coefficients that JMP is generating is
| Term | Estimate |
| AR1,1 | -0.0447 |
| AR1,2 | -0.0061 |
| AR2,12 | 0.15059 |
| MA1,1 | 0.72949 |
| MA2,12 | 0.93074 |
The above coefficients when plugged in the above formula is generating very erroneous forecasts.
And the formula given in literature is very different to formula given in JMP ARIMA Models which I am unable to understand.
Can somebody help in deciphering the formula given in JMP with that given in literature?
Regards
Ramesh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mathematical Equation to Forcecast with SARIMA Model
The formula that you gave is not correct, by just looking at the maximum lag. If you are really into finding the truth about SARIMA formulas, I recommend that you check out the book "Time Series Analysis: Forecasting and Control", by Box, Jenkins, and Reinsel. ARIMA models are also known as Box-Jenkins models, that is why.
Now talk about (2,1,1)(1,1,1)12 model. First let me get the name right to facilitate the explanation: (p=2,d=1,q=1)(P=1,D=1,Q=1)S=12.
There are totally six polynomials: two for AR part (involving p and P), two for MA part (involving q and Q), two for differencing part (involving d and D).
Start with the differencing part, which is the product of two polynomials: (1-B)(1-B^12). This means the series is preprocess by differencing: Z[t] = Y[t] - Y[t-1] - Y[t-12] + Y[t-13].
Then the series Z[t] is modeled by an SARMA model, notice the "I" in the middle is gone.
Now look at the AR part, which is the product of two polynomials: (1 - phi1* B - phi2* B^2)(1 - phi3* B^12). Expand it I get: (1 - phi1* B - phi2* B^2 - phi3* B^12 + phi1*phi3* B^13 + phi2*phi3*B^14).
Now look at the MA part, which is the product of two polynomials: (1-theta1 * B)(1- theta2*B^12). Expand it I get: (1-theta1*B-theta2*B^12+theta1*theta2*B^13).
Now put AR polynomial and MA polynomial in the equation:
(1 - phi1* B - phi2* B^2)(1 - phi3* B^12). Expand it I get: (1 - phi1* B - phi2* B^2 - phi3* B^12 + phi1*phi3* B^13 + phi2*phi3*B^14)Z[t] = (1-theta1*B-theta2*B^12+theta1*theta2*B^13)a[t].
Now put Z[t] on the left side of the equation, and all other terms on the right:
Z[t] = (phi1* B + phi2* B^2 + phi3* B^12 - phi1*phi3* B^13 - phi2*phi3*B^14)Z[t]+ (1-theta1*B-theta2*B^12+theta1*theta2*B^13)a[t]
Now apply back operator rules, and get:
Z[t] = (phi1* Z[t-1] + phi2* Z[t-2] + phi3* Z[t-3] - phi1*phi3* Z[t-13] - phi2*phi3*Z[t-14]+ a[t]-theta1*a[t-1]-theta2*a[t-12]+theta1*theta2*a[t-13]
Notice a[t] = 0. Z is the differenced series, which you should be able to calculate from Y series using the formula that I mentioned about. the remaining a values are innovations from the fitted model. So, you should be able to get Z[t] now.
Now look at Z[t] = Y[t] - Y[t-1] - Y[t-12] + Y[t-13] again. Re-arrange it, and I get Y[t] = Z[t] + Y[t-1] + Y[t-2] - Y[t-13]. So I can get Y[t] given all previous Y's and Z[t].
The explicit formula of Y[t] is far more complicated than the formula that you provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Mathematical Equation to Forcecast with SARIMA Model
Thank you sir for the detailed explanation. Much obliged.
Indeed, the explicit formula is far more complicated and I am not sure if it can be manually calculated.
Regards
Ramehs
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us