- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Long shot: How to use numpy.polyfit to reproduce Vec Quadratic() results?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Long shot: How to use numpy.polyfit to reproduce Vec Quadratic() results?
Apologies for the transgression, which is; ironically; a direct result of my personal progress in JSL.
A very helpful computer scientist in my organization is trying to translate something initially written in JSL to Python. Specifically, the challenge is how to reproduce what the JSL function 'Vec Quadratic()' is doing? See also the attached example table .
Background:
The JSL application to be translated creates formula columns for the confidence and prediction intervals. The formulas are then used to calculate the values of the confidence and prediction intervals for some user specified value of x, aka independent variable.
Questions:
- Is numpy.polyfit (https://numpy.org/doc/stable/reference/generated/numpy.polyfit.html) the right choice for this?
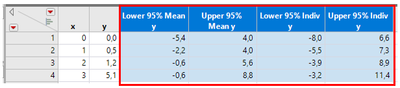
- If it is, anyone who knows how to use numpy.polyfit to reproduce the results for Lower & Upper 95% Mean & Indiv columns in the attached table or can point us into the right direction?
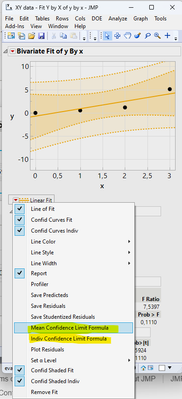
Screenshots for orientation:
- What we want to achieve in Python (results inside the red frame)
- How the columns shown above were generated
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Long shot: How to use numpy.polyfit to reproduce Vec Quadratic() results?
... you notice that it has some issues with matrix manipulations :)
after adjusting the brackets, you get:
import numpy as np s = np.array( [[1.,3.,5.],[3.,2.,6.], [5.,6.,1.] ]) x = np.array( [[1.,3.,5.],[2.,4.,6.] ]) res= x @ (s @ x.T) print(res) print(res.diagonal())
... which fits to
Names Default To Here( 1 );
exS = [1 3 5, 3 2 6, 5 6 1];
exX = [1 3 5, 2 4 6];
Print(r= exX * exS * exX`);
tmp=as list(r);
print(tmp[1][1],tmp[2][2])
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Long shot: How to use numpy.polyfit to reproduce Vec Quadratic() results?
@Ressel I think the confusing part of your request is that Vec Quadratic() is simply performing matrix math as described by the Scripting Index. The results of Vec Quadratic() is simply the output of matrix operations.
The formulas themselves, which give the 95% values, are generated by the Fit Y by X platform. 'Fit y By X' is also what is responsible for creating the plot. So the question as I understand it, is more accurately; How do I do a Bivariate Fit of y By x with confidence levels in Python or numpy?
I think the Vec Quadratic() is the wrong focus since it didn't create the formula or the constants, it's just a mathematical operation in the generated formula.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Long shot: How to use numpy.polyfit to reproduce Vec Quadratic() results?
@Paul_Nelson, this is correct, which I only figured out later (and shamelessly exploited to accept my own answer as solution). With regards to this as well as the exact phrasing of the question, I honestly didn't have it in me. The more one learns ... Thank you very much for sharing & have a good weekend.
(P.s.: As a sophisticated, statistical software company you'd almost count on engineers without computational talent being part of the business model. For better or worse.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Long shot: How to use numpy.polyfit to reproduce Vec Quadratic() results?
I applaud the openness of Jmp for Python :)
As @Paul_Nelson mentions - now with Jmp18, if a functionality is missing in JMP, every user can easily grab it from Python - with 2-3 lines of code. amazingly useful!
On the other hand, some Wikipedia knowledge about matrix manipulation, DOEs, regression, neural networks, etc. is nothing to worry about being "stolen".
With the "functionality" coming from state-of-the-art, up-to-date Python packages, it will be the "soft skills", the absence of bugs, the intuitive interface, the superior user experience that will speak for JMP and separate it from the competition:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Long shot: How to use numpy.polyfit to reproduce Vec Quadratic() results?
Moreover, I think it's only natural that users getting into data analytical & automation work via JMP are unlikely to have a firm grasp of Python, or any other programing & scripting language for that matter. JMP is proactively trying to recruit this type of user and makes it (I think) easy to step into scripting in JSL. Once the user develops and learns, though, this can be expected to trigger the wish for additional knowledge, at least in some cases and after the initial barrier of understanding a few basic, computational concepts is overcome. Of course the first intuition for this kind of user will be to ask the community for help, especially after the advertised Python integration in JMP 18. Finally, the fact that a professional data scientist is tasked with copying what a lay statistician has developed in JMP for use in an actual business setting speaks for itself. Although, I might be getting it all wrong.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Long shot: How to use numpy.polyfit to reproduce Vec Quadratic() results?
If anyone's interested, the below Python code looks like it will exactly reproduce what JMP is doing in terms of calculating the confidence interval around a regression. This code block can be pasted into a Jupyter notebook directly. Besides calculating the Y- coordinates of the confidence interval for every X in the linear regression it does also create a plot, calculates the regression coefficient, intercept, associated uncertainties and tabulates the results.
Don't believe I wrote this myself, but still useful for learning.
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
# the data as array
x_coordinate = np.array([0, 1, 2, 3])
y_coordinate = np.array([0.0, 0.5, 1.2, 5.1])
# linear model
func = lambda x, a, b: a * x + b
# model fit
best_fit_ab, covar = curve_fit(func, x_coordinate, y_coordinate)
sigma_ab = np.sqrt(np.diagonal(covar))
# extract fitted parameters and uncertainties
a, b = best_fit_ab
a_err, b_err = sigma_ab
text_res = f"Best fit parameters:\na = {a:.10f} ± {a_err:.10f}\nb = {b:.10f} ± {b_err:.10f}"
print(text_res)
# calculate the standard error of the regression
residuals = y_coordinate - func(x_coordinate, a, b)
s_err = np.sqrt(np.sum(residuals**2) / (len(x_coordinate) - 2))
# define a function to calculate the confidence intervals
def predict_ci(x, func, popt, pcov, s_err, alpha=0.05): # adjust alpha here
from scipy.stats import t
df = len(x_coordinate) - 2
t_val = t.ppf(1 - alpha / 2, df) # t-value for the given confidence level and degrees of freedom
y = func(x, *popt)
ci = t_val * s_err * np.sqrt(1/len(x_coordinate) + (x - np.mean(x_coordinate))**2 / np.sum((x_coordinate - np.mean(x_coordinate))**2))
return y - ci, y + ci
# generate points for high-resolution x-axis
hires_x = np.linspace(x_coordinate.min(), x_coordinate.max(), 100)
# calculate confidence intervals
ci_lower_orig, ci_upper_orig = predict_ci(x_coordinate, func, best_fit_ab, covar, s_err)
# tabulate the original data and confidence intervals
table_orig = np.column_stack((x_coordinate, y_coordinate, ci_lower_orig, ci_upper_orig))
print("\nTabulated values (original data):")
print("X Coordinate\tY Coordinate\t\tCI Lower\t\tCI Upper")
for row in table_orig:
print(f"{row[0]:.2f}\t\t{row[1]:.10f}\t\t{row[2]:.10f}\t{row[3]:.10f}") # adjust decimals for tabulation
# plotting the data
plt.scatter(x_coordinate, y_coordinate, label='Data', color='blue')
# plotting the fitted model
plt.plot(hires_x, func(hires_x, *best_fit_ab), 'black', label='Fitted model')
# plotting the confidence intervals
ci_lower, ci_upper = predict_ci(hires_x, func, best_fit_ab, covar, s_err)
plt.fill_between(hires_x, ci_lower, ci_upper, color='black', alpha=0.15, label='Confidence interval')
# adding text with parameters
plt.text(x_coordinate.min() + 0.5, y_coordinate.max() - 0.5, text_res)
# customize plot
plt.xlabel('X Coordinate')
plt.ylabel('Y Coordinate')
plt.title('Y Coordinate vs. X Coordinate')
plt.legend()
plt.show()
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us