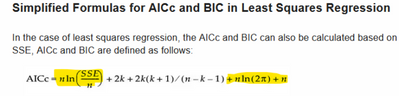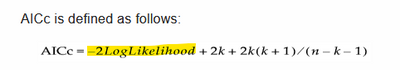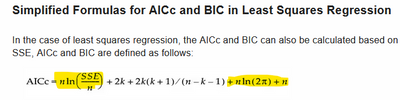- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Loglikelihood for normal OLS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Loglikelihood for normal OLS
Hi JMP Community!
I'd like to view the Loglikelihood of my linear model (Fit Model -> Personality: Standard Least Squares). I do get the AICc with the corresponding option in "Regression Reports". But how can I extract the loglikelihood?
I found also this thread: https://community.jmp.com/t5/Discussions/AICc-log-likelihood-where-is-it-reported/td-p/272033?trMode...
However I could not reproduce the AICc with this -2LL formula.
Thanks for your help!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
rmse = 0.421637;
k = 3;
n = 18;
mse = rmse^2;
SSE = mse * (n - k);
//all above uses k=3, for 3 regression coefficients.
k = k+1;
//the above increases the number of parameters by 1, which is the sigma.
AICc = n * log(SSE/n) + 2*k + 2*k*(k+1)/(n-k-1) + n*log(2*pi()) + n;- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
Hi @Halbvoll : Consider the complete model; in addition to the regression coefficients, there is Sigma (recall part of the model is the error term, distributed Normal[mean=0, Sigma] ). So, Sigma (estimated by the RMSE) is the additional parameter in the model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
@Halbvoll and @MRB3855 thanks for the followup discussion.
@Halbvoll I had the same concern when I posted my answer. @MRB3855 the sigma in the AICc for Least Squares is not RMSE, which I was confused initially as well. After communicating with a developer who has better knowledge on the subject, I now can explain what is going on, as follows.
- Least Squares does not estimate sigma as a free parameter. So the number of parameters in a Least Squares is the same as number of regression coefficients.
- The Least Squares estimate of Sigma is RMSE, which is sqrt(SSE/DF), where DF = Number of Observations - Number of Coefficients. This Sigma is not a free parameter in the sense of statistical estimation.
- The AICc formula uses the likelihood, which is based on the normal density function with Sigma, whose MLE is sqrt(SSE/N). The first term in the following screenshot is the contribution from Sigma's MLE. In such sense, when computing AICc in this way, the number of parameters must count Sigma in addition to regression coefficients.
I was pointed to the following article to see the full proof and complete derivation. If you are interested, see all the derivations up to Eq 6.
https://www.sciencedirect.com/science/article/pii/S0893965917301623?ref=cra_js_challenge&fr=RR-1
H.T. Banks and M. L. Joyner, 2017, AIC under the framework of least squares estimation, Applied Mathematics Letters, Volume 74.
We will take care of the clarification in a future version of the documentation. Thanks again!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
Hi @Halbvoll : If you have AICc or BIC, algebra (via the formulas here https://www.jmp.com/support/help/en/15.1/index.shtml#page/jmp/likelihood-aicc-and-bic.shtml#ww293087) will give the the Loglikelihood:
LL=(kln(n) - BIC)/2
or
LL= (2k+2k(k+1)/(n-k-1) - AICc)/2
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
Hi @MRB3855 ,
thanks for your answer! Indeed - I already calculated the LL that way. However, I double-checked the LL with other softwares/python packages (using the exact same data and model params) and got a different LLs, although the R2, SSE, RMSE etc. is exactly the same. Especially with a higher number of k the LL tends to have a bigger difference between JMP and i.e. Python package Statsmodels (PpS).
So this is what confuses me, PpS and JMP should use the same formula for the AICc but I get different results (since the LL is probably different).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
@Halbvoll they may not use the same formula. JMP's version is the modified version, to adjust for small sample sizes. And since you say "Especially with a higher number of k the LL tends to have a bigger difference between JMP and i.e. Python package Statsmodels (PpS)", I suspect that Python is using the unmodified version; so you may want to check your assumption that they are using the same formula.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
hi@MRB3855 ! When you speak of formula, you mean the formula for the AICc, right? I've checked that too. I've re-implementated JMPs AICc formula in Python using the LL I get from statsmodels. However, I get the same AICc as using the AICc function from statsmodels. So the issue is, that the LL between statsmodels and JMP is different and I would like to know why.
Or do you speak of the LL formula? If so, I couldn't figure out how JMP is calculating the LL but this would be the key to my questions.
Thanks for your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
@Halbvoll, have you tried the Fit Model -> Personality: Generalized Linear Model, Distribution: Normal, Link Function: Identity?
The output report includes -(LL) for the full and reduced model.
Hopefully this is helpful for you.
Sincerely,
MG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
How do you calculate -2LL for your model?
JMP often uses the kernel density function when optimizing the parameter estimates. This approach is justified because -2LL and AICc have no meaning or interpretation in any absolute sense. They are used on a relative basis to compare models, so the kernel is sufficient. Try using the kernel density instead.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
Maybe this page can help: https://www.jmp.com/support/help/en/15.1/index.shtml#page/jmp/likelihood-aicc-and-bic.shtml#ww293087
Scroll down to the bottom to see the formula related to least squares.
Notice the relationships among the pieces in three sets of formula:
(1) from the top half of that page
(2) from the bottom half of that page
(3) from the thread that you point to
So the -2Loglikelihood in (1) equals the two highlighted pieces in (2).
And the -2Loglikelihood in (1) and (2) are different from (3) by a constant N.
In other literature, you may see -2Loglikelihood = N*log(SSE/N). I am glad that you notice the difference. It is common in the literature that constants in loglikelihood get dropped off.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
Thanks all for your support!
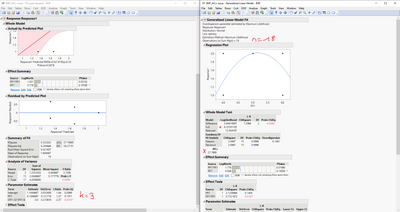
Thanks for pointing that out @modelFit ! This was the option I was looking for. For my data, I get the same LL as with statsmodels - which confuses me even more. Maybe my issue becomes more clear with a screenshot (I hope the resolution is high enough) of my problem:
Therefore, I have the following results based on JMP 16.2.0:
- -LL = 8.3501
- k = 3
- n = 18
- AICc = 27.7869
However, if I use -LL, k and n to calculate the AICc manually (formula (1)) I get 24.4243 -> I get the same result with statsmodels.
If I use JMPs AICc and re-formulate the formula to LL= (2k+2k(k+1)/(n-k-1) - AICc)/2 I get an -LL of 10.036.
Something doesn't add up, or am I missing something?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
rmse = 0.421637;
k = 3;
n = 18;
mse = rmse^2;
SSE = mse * (n - k);
//all above uses k=3, for 3 regression coefficients.
k = k+1;
//the above increases the number of parameters by 1, which is the sigma.
AICc = n * log(SSE/n) + 2*k + 2*k*(k+1)/(n-k-1) + n*log(2*pi()) + n;Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us