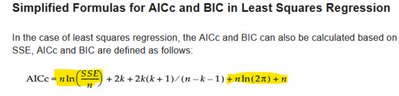- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Loglikelihood for normal OLS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Loglikelihood for normal OLS
Hi JMP Community!
I'd like to view the Loglikelihood of my linear model (Fit Model -> Personality: Standard Least Squares). I do get the AICc with the corresponding option in "Regression Reports". But how can I extract the loglikelihood?
I found also this thread: https://community.jmp.com/t5/Discussions/AICc-log-likelihood-where-is-it-reported/td-p/272033?trMode...
However I could not reproduce the AICc with this -2LL formula.
Thanks for your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
Thanks @peng_liu !! This is the missing info which resolves my issue! Would it be worth to enhance JMP's documentation on that point? Because in the documentation k is described as follows "where k is the number of estimated parameters in the model " (https://www.jmp.com/support/help/en/17.1/index.shtml#page/jmp/likelihood-aicc-and-bic.shtml ) which led to my confusion.
Also, in the publications referenced in the documentation, I have always understood k to be the number of parameters. Where does this k+1 come from before the actual AICc calculation? Is there a specific publication describing this procedure?
Edit: could it be that the formula is based on this publication? https://sites.warnercnr.colostate.edu/wp-content/uploads/sites/73/2017/05/Anderson-et-al-1994-Ecolog...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
Hi @Halbvoll : Consider the complete model; in addition to the regression coefficients, there is Sigma (recall part of the model is the error term, distributed Normal[mean=0, Sigma] ). So, Sigma (estimated by the RMSE) is the additional parameter in the model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
@Halbvoll and @MRB3855 thanks for the followup discussion.
@Halbvoll I had the same concern when I posted my answer. @MRB3855 the sigma in the AICc for Least Squares is not RMSE, which I was confused initially as well. After communicating with a developer who has better knowledge on the subject, I now can explain what is going on, as follows.
- Least Squares does not estimate sigma as a free parameter. So the number of parameters in a Least Squares is the same as number of regression coefficients.
- The Least Squares estimate of Sigma is RMSE, which is sqrt(SSE/DF), where DF = Number of Observations - Number of Coefficients. This Sigma is not a free parameter in the sense of statistical estimation.
- The AICc formula uses the likelihood, which is based on the normal density function with Sigma, whose MLE is sqrt(SSE/N). The first term in the following screenshot is the contribution from Sigma's MLE. In such sense, when computing AICc in this way, the number of parameters must count Sigma in addition to regression coefficients.
I was pointed to the following article to see the full proof and complete derivation. If you are interested, see all the derivations up to Eq 6.
https://www.sciencedirect.com/science/article/pii/S0893965917301623?ref=cra_js_challenge&fr=RR-1
H.T. Banks and M. L. Joyner, 2017, AIC under the framework of least squares estimation, Applied Mathematics Letters, Volume 74.
We will take care of the clarification in a future version of the documentation. Thanks again!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Loglikelihood for normal OLS
Hi @peng_liu , thank you very much for the detailed explanation and this publication, I was not familiar with this paper until now. And thanks for updating the documentation in future!!
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us