Least squares regression for nonlinear system of equations

[#1]

Hello - I have a moderately complex model for a physical process (ion adsorption for anyone who knows what that means). I have two starting variables, x1 and x2, and two measured outcomes, y1 and y2 that change with x1 and x2, and unmeasurable, or hard to measure, variables, g1,...,gn that don't change. One or both of x1 and x2 can also change for each row in a series. I have a set of nonlinear equations, s = f(x1, x2, y1,...,y2, g1,...,gn), as well as some other functions of different variables in f, depending on how complex I want the model to be. See the attachment for example equations.

The typical way we do this is in Matlab with lsqnonlin. Works well, but it's a bear to get running. I'd much rather have a (not-so-simple) column formula. However, I'm not entirely sure how to code it. The nonlinear regression thing is built for single equations, and with the three equations that all describe the same s, it seems like recursion would abound. I'm also not sure what the loss function would be. In matlab, we input guess values, calculate the least squares between the guess and the calculated value, update it if the sum of squared differences of all the guesses and equations falls outside some tolerance, and then loop. I'm assuming this is done internally by the nonlinear platform, but then is my target zero since I want the sum of squared differences to be zero? Or if not, how do I do multiple equations?

Apologizes if this is way simpler than I'm thinking.

[#2]

One way that I suggest is an old trick by defining an appropriate lost function. In your case the lost function can be:

(s-f1(...))^2 + (s-f2(...))^2 + (s-f3(...))^2 + ...

Each element is the squared error of an equation in your systems. You sum them up, and minimize the overall error. This approach converts a nonlinear least squares problem to a loss function optimization problem.

Meanwhile, I think it is still doable using nonlinear least squares for a system of equations. Here are the steps:

1. Expand your data table. For each row, you make copies of it, and the total number of copies the the same as your number of equations in your system. This add-in might be useful for this task. You need to create a Freq column, whose cell values are the number of equations.
2. Now you need to create that not-so-simple formula column. Depending on how your arrange the rows from the last step, you may need to write the formula differently. But the goal is the following. For each copy of the original row, assign it to one equation in your system. So, in the end, every copy of a row is associated with a distinct equation in your system. You probably need to figure out how to associated row number with equation number. If the copies are in consecutive rows, as the result from the above add-in, you may need the "Modulo" function to make the mapping.

In the end, use the Nonlinear as you know to solve the least squares problem.

[#3]

Hi @peng_liu thanks for the answer and sorry for the delay in response! Dissertation + 2 month old baby make you forget to follow up on things.

What would you chose as the s? I don't have any s measured, and in the matlab code, we guess an s, and then update. How would you suggest doing this? 

As for the least squares method, that looks interesting. Do you have a table you've made for another project I could look at that does a similar thing? For all my scripting, I've not done much with row based formulas and I've failed spectacularly when I have. 

[#4]

Congratulations!

So, "s" is an unknown parameter here. In that case, rewrite all your equations to something like this: 0 = f(...) - s.

Or if you have known quantities in your equations, move them to the left hand side. The left hand side will be your Y when you use the Nonlinear platform.

I have no examples, so I made up one. Attached: nonsense system of eqns.jmp

It has

1. a Y column, known quantities.
2. a formula column, the stuffs on the right hand size of your equations
3. a label column indicates odd rows are corresponding to the first equation and the even rows are corresponding to the second equation
4. other known quantities that are part of the equation on the right hand side.

Look at the formula in the "formula" column to see how to dispatch two equations in a single column.

[#5]

Thanks for the guidance @peng_liu!

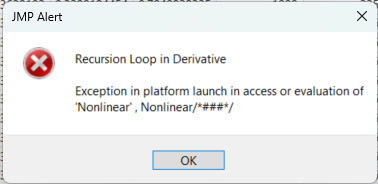
I've put together a table and it seems to work if I have a couple of rows, but if I try to do more than a few, it gives me this: 

Is this indeed an issue with just having too many rows? The error seems to persist if I cut down the rows to the minimum (3 in this case) and I have to go make a new table. Do you have any thoughts on this? Here's the table I've made with a barebones version of the model so its not cumbersome. I've also put the parameters into their own columns (Phi0, sigma0, pHf) and expanded intermediate formulas to make looking at the column formula easier.

[#6]

I am not sure how to run Nonlinear platform using this data table. Which is Y, which is X?

But if "Formula" column is X, I don't think it would work. The formula of X must use Parameters, not Table Variables.

The following is what the X column looks like in that "nonsense data table".

Your "Formula" column does not have anything listed under Parameters.

[#7]

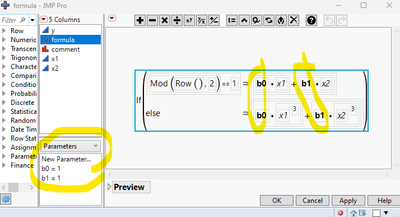
Hey @peng_liu - Yea so because the parameters were making the formula 100 times as long, I dumped them into the Phi0, sigma0, and pHf columns (columns 6-8 after the column with a "." as the title), and then was selecting the "Expand intermediate formulas" box at the bottom of the nonlinear platform. That way I can use the parameters but they aren't making the formula column impossible to work with, since there are so many "expanded categories" for each parameter.

Does that make sense? 

The attached screenshot should show those columns and their location in the formula, in case that makes it clearer.

[#8]

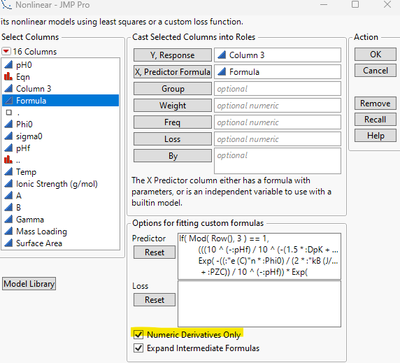
@peng_liu I will also say that I've found that 1) numerical derivatives only option does seem to get it to go through to the main platform, and 2) that when I have parameters in more than one of the equations, it seems to give that error. Not sure if that tells you anything. I just can't find a reference to that error so I'm stumped.

[#9]

Thanks for explaining, @ehchandlerjr I understand what you are doing now. What you are doing is a nice trick for such a complicated problem. Something new to me!

I looked at the error message. You need to check "Numerical Derivatives only".

You have 300+ parameters, the underlying symbolic derivative is hitting a limit.

I see you have 337 rows, but 339 parameters. This subset won't get a solution. Hope your full set does not have the issue.

Meanwhile, while I am looking at your setup, something is interesting. I don't know your subject. But in your setup, Phi0, sigma0, and pHf are discrete functions of pH0. Are the relationships between the three and pH0 known? If continuous relationships (with fewer unknown parameters) are known among them, you might largely reduce the number of parameters.

[#10]

@peng_liuok that makes more sense. Do you happen to know the limit on number of terms or parameters in the symbolic derivative code? Because I'm thinking I can just have a column with a few numbers and then segment the calculation using the "by" feature. The symbolic derivative is just so much faster.

And hmmm. Not sure where the new parameters came from. I'll check it when I get in. Thanks for noticing that. Three related questions: 1) how did you see the number of parameters and 2) is there a way to bulk delete parameters when in the column formula menu? As far as I can tell, you have to right click, click delete one by one. 3) is there a way to use a table to input the parameters and their bounds? This would really help speed.

Thanks!