- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- K-means cluster with correlated inputs
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
K-means cluster with correlated inputs
Hi all,
I'm working with a system where I need to do both variable reduction and clustering. I am studying fish behavior. I have three behavioral treatments and when I look at a PCA biplot its obvious that my data clusters into two groups and they roughly correspond to my lowest and highest treatment categories. I have an intermediate category that is split between the two. I want to use K-means to consolidate my treatment variable into two treatments instead of three to be used in later analyses.
Two questions:
1: If I am using multiple very similar highly correlated inputs (several different ways to measure body curvature) does that mess with the clustering algorithm? Should I be doing my variable reduction before clustering?
2: I received reviewer comments saying "these clusters don't mean anything, of course a clustering algorithm is going to find differences" is there a way to address these comments referencing the way K-means clusters works.
Thanks,
Stephen
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: K-means cluster with correlated inputs
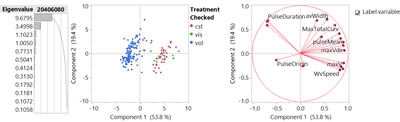
Hi Stephen2020 - You have very strong PCA results looking at the picture included. This is your statistical support for two groups. K-means uses the PCA results, so you've done variable reduction as part of doing K-means.
In the Principal Components platform, do a Bartlett Test for significance of your Eigenvalues. When you do K-means, you see these Eigenvalues under the bi-plot. If nothing is significant with the Bartlett test, you won't get very good groups in K-means. Likewise, if you don't have Eigenvalues that explain much of the variation, you don't really have much correlation structure and variable reduction isn't doing much (and hence K-means won't magically produce clear groupings).
You can use the CCC to test for other numbers of clusters, and if you get 2 this would be additional support that 2 is a good number of clusters. The CCC is the Cubic Clustering Criteria and try a range of clusters, like 2 to 5. The documentation has a reference for this method. If you don't get 2, it's not a strong justification for NOT using 2 groups (because your expertise is guiding your choice of 2 groups). CCC is a guide and supporting evidence only.
Finally, use the means and standard deviations reported for your groups in K-means. Do the standard deviations overlap between clusters (high of one overlap with low of the other - you'll have to calculate this)? If not, then you can make a statement about that as well.
The one cautionary note is that anything you put into PCA and K-means can't be later pulled out and used as a Y variable for further analysis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: K-means cluster with correlated inputs
Thanks for your help, this gives me a lot to work with. Can you further explain your note of caution? I have a set of (9) input and (9) output variables. Currently I am throwing all of them into the K-means cluster. Identifying clusters using K-means effectively reduces my number of treatments from 3 to 2. Then I would use the "cluster variables" tool to identify representative input and output variables (as a form of variable reduction) and then use those representative variables to build my model. I would be building a separate model for each data cluster. If I simplified it and said I had one input and one output, used them both to identify clusters then regressed the input and output within each cluster, would I be using the data improperly?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: K-means cluster with correlated inputs
I'm a bit lost in what you're doing, and your ultimate goal. Which that in mind, here are some things to consider.
You say have 9 inputs (Xs) and 9 outputs (Ys). You're also changing something for a treatment - is this one of these 18 variable?. I don't understand what're ultimate model will represent - the Xs vs the Ys, or 18 variables versus something else like the treatment?
You can definately use clustering techniques, like K-means, to segment your data (so which rows go together) and build a model from each subset of your data. Typically people don't use the results of the clustering in the actual model if you're segmenting, other than to divide up rows. You can do further dimension reduction on each segment independently - which means you've decided to treat each segments of your data independently.
Using Variable Clustering to identify leading variables for your model is a related, but different way to cluster compared to K-means. So you're doing two different clustering methods and it's not clear how you used them together. You most certainly don't use Variable Clustering on future Y variables. They need to stay out of the analysis until you model. Likewise, if you do K-means with all 18 variables (X's and Ys), split the data in 2 based on this, then run a model on each section, just realize you've biased your outcome because of allowing the relationships between Xs and Ys to be considered before making another model. Cluster on Xs, if you're going to use them in a model, not the Ys.
Overall, when using dimension reduction techniques on a group of variables, if you're going to use these as Xs in a further model, you don't put your future Y variable in there. The point of running a model is to have some Xs explain what is going on for a Y variable(s) of interest. If you PCA or cluster these Xs and Ys together, you're confounding why you'd do a model in the first place.
Here are a few other ideas, depending on your goals.
There is a way to do variable selection with a Y on X's - use Partition, or another tree method like Bootstrap Forest. This would give you the variables that rank highest with respect to a Y, and you can ignore other Xs of small to no effect. Then take these Xs and build a model in Fit Model.
You can also do dimension reduction on some of you variable - like all the body curvature. You'd do PCA, and use the top PCA components in the model (say 9 curvature measurements could be explained in 3 PCA components). Then use the PCA components as Xs in the model. Again don't include the future Ys in the PCA. This is nice cause the PCAs are orthogonal which is an assumption of linear modeling.
If you have JMP Pro, you can use LASSO in GenReg to do both variable reduction and fit a model at the same time. There are limits to how complex this model can be. You can use a tree method first to cut down the number of variables.
Also, because you said you have behavior data, you might consider using GenReg to fit a model because it has some resampling methods for small data sets.
If you're looking at 9Xs and 9Ys, you might want PLS.
Finally, perhaps what you are trying to do is actually a Discriminate Analysis. If you're trying to build a model that describes Treatment with all 18 variables, then Discriminate Analysis is a categorical regression with variable reduction and quite appropriate for this. You can run DA with 2 or 3 treatments and compare the fits to decide if you have 2 or 3 groups.
There are Masting JMP topics on all of the items I've mentioned above.
Have you watched this video on multivariate analysis? There is also a journal that goes with the video.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us