Calculating contribution to variance in a GLM

[#1]

Hello,

When I run a simple GLM with say 4 terms I would like to know the percent contribution of each term to the model.  Here is an example:

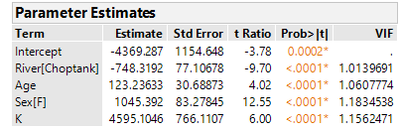
I constructed a simple model that includes river, age of fish, sex of fish and condition factor K as independent variables.  I would like to know what the contribution of each of these terms is to the overall variance in the model.  I read that 1 basic method is to divide the sum of squares for each term by the total model-wide sum of squares and multiply by 100.  Is that correct?  I have the following:

 and 

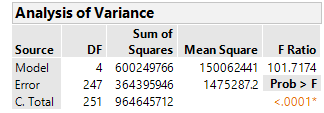
The error source above is the residual sum of squares, correct?  So I would divide each of these sums of squares, including error, by 964645712, which is the total sum of squares (model plus error).  However, when I do this the percentages only add up to 84% and not 100%.

So, am I on the right track or is there a better method?  Ultimately I would like to know what term has teh most influence on changes to my dependent variable.

Thanks!

[#2]

By default JMP uses Type III Sums of Squares, which are not additive. The Type III Sum of Squares quantify the amount of variability that the term explains once all of the other terms are accounted for. It seems that you would like to have the Type I Sum of Squares, which are additive.

To see those, click the red triangle by the Response menu title. choose Estimates > Sequential Tests. Please note that the sequential tests are now order dependent. This means that the model of River, Age, Sex, and K will give you different sums of squares than the results where the model is specified as K, Sex, Age, and River (as one possible example). This is why they are not the default for JMP.

I think you are looking to determine which terms in the model are most important and rank order that importance. But importance could be looked at in a couple of ways. First, could be which terms are most significant. For this, you should consider the Effect Summary which provides a bar chart to illustrate how significant each term is to the model. Second approach to importance would be to consider which terms affect the response the most. You can determine this visually with the Prediction Profiler. Note that there are other possible tools for each of these approaches and probably even other ways to consider importance.