- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: JSL Constrained Minimize - Row by Row Solver Help
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
JSL Constrained Minimize - Row by Row Solver Help
Hi There,
My objective is to have JSL iterate through values in two columns (x1, x2) which is are used in formulas of other columns until it meets the criteria of [column(y1)- column(y2) = 0 ;column(z1)-column(z2)=0]. Note that the equation I'm trying to solve is a nested non-linear equation where
y1 = f1(x1, x2, x3, x4...)
y2 = f2(x1, x2, x3, x4...)
z1 = y1+y2
z2 = independent value
In Excel, it was simple enough to just break down the equation into multiple columns to more easily track if there were any calculation errors in between. Then iterate through each row and do a solver to iterate x1 and x2 until the objective criteria is met.
In JMP, I'm having difficulties using the Constrained Minimize function to replicate this. Everytime I run the script, its does not look like its converging because the target objective is not met and the values are constantly changing. Also I can only set 1 target objective rather than 2. Below is an example of my JSL code. Note that column_y1 and column_y2 are formula columns that have x1 and x2 variables inside.
dt = Current Datatable();
expr1 = abs(:column_y1[i] - :column_y2[i]);
x1 = 0.5;
x2 = 0.2;
For Each Row(
i=Row();
minfun = Constrained Minimize (expr1, {x1(0.1,0.8), x2(0.01,0.5)},
<<MaxIter(100000),
<<ShowDetails(True)
)
Show(x1, x2, minfun);
column(dt, "column_x1")[i] = x1;
column(dt, "column_x2")[i] = x2;
);
Do you think I need to have the ENTIRE nested equation in the expression for this to work? Or is there something wrong I'm doing here.
Any help is greatly appreciated. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JSL Constrained Minimize - Row by Row Solver Help
Hi Peng Liu,
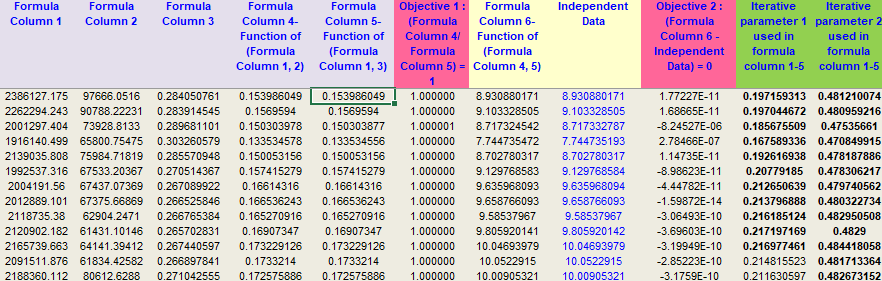
I'm not sure if this helps because I have to anonymize the data, but basically this has been what I was trying to replicate or improve upon from Excel:
In this case, I'm using a macro + Excel's solver to iterate parameter 1 and parameter 2 to reach objective 1 and objective 2
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JSL Constrained Minimize - Row by Row Solver Help
In this case, I don't think solving multiple equations simultaneously is the direction to go, because every row in your table involves two variables: parameter1 and parameter2. And they are different variables from row to row, though they have the same name from equation to equation and you put them under the same column.
For simultaneously solving multiple equations using the suggestions that I gave, equations use the same set of variables from equation to equation. Every variable should have just one value.
What you need to do is to translate what you have done in Excel Macros to JSL, e.g. you need to write a bigger JSL loop to go through every row iteratively.
For solving equation under a nonlinear constraint, one of my suggestions was to convert a constrained problem to an equivalent unconstrained problem. Assume your constraint is an equality, the following example tries to find the solution to y-exp(x)=0, under constraint y==exp(-x). The solution is the intersection of the two curves, which is at (x,y)=(0,1). The minimizing objective is sum of squared errors of the target equation y-exp(x), and the violation of the constraint y-exp(-x)=0. Notice k is a penalty on the violation , and k is rather large.
Also notice, I intentionally put the initial values far away from the solution, and increase MaxIter, just in case you cannot identify initial values that are not close to the solution.
x = 100;
y = 100;
k = 10000;
minFun = Minimize( (y - exp(x))^2 + k*(y - exp(-x))^2, {x, y} , MaxIter(1000));
Eval List( {x, y, minFun} );
show(x, y, y-exp(x),y - exp(-x))It is a feasible approach if your actual objective can use.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JSL Constrained Minimize - Row by Row Solver Help
Hi Peng Liu,
Thank you very much for your persistence in helping me resolve this issue. I referenced how you converted it to an equivalent unconstrained problem then minimizing the sum of squared errors of both the target equation and the constraint. While I did not need to use a penalty term, the solution more or less matches what I see in Excel.
It takes about 2-3 minutes to solve for 1100 rows of cases (which I think is absolutely reasonable given how convoluted my equations are), after I set it such that the starting value begins from values solved from the previous row of data.
Again, many thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JSL Constrained Minimize - Row by Row Solver Help
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us