- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Use of goodness of fit statistics in Poisson GLM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Use of goodness of fit statistics in Poisson GLM
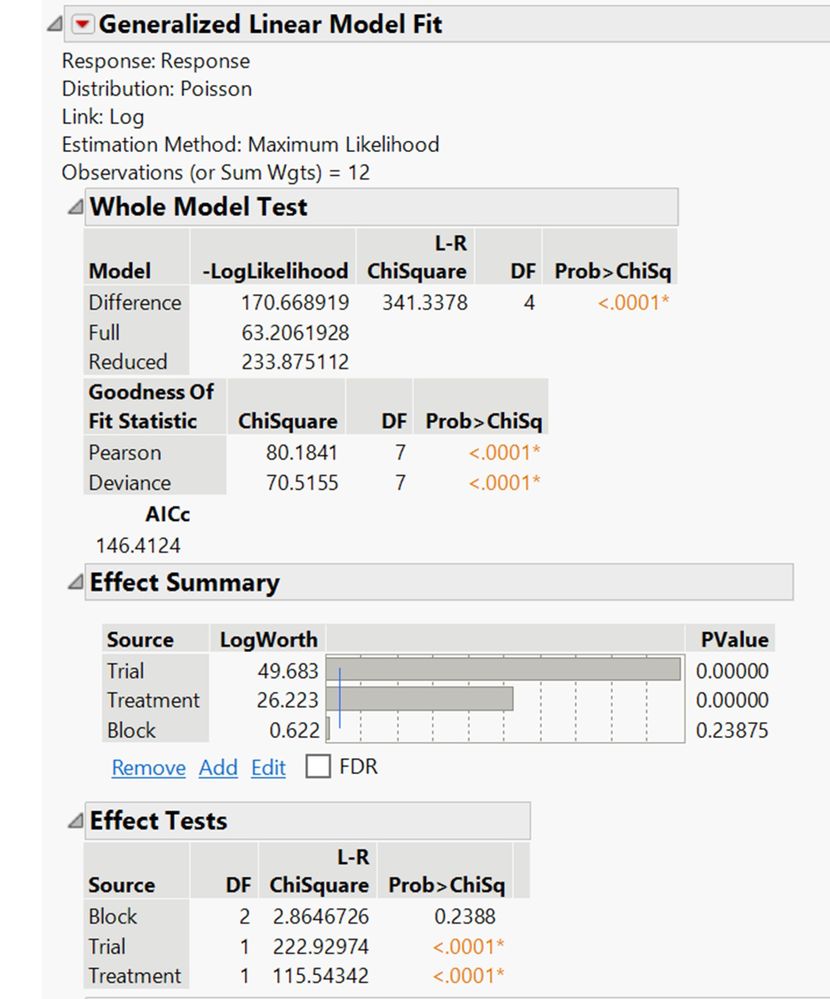
I'm using JMP Pro 15 to run a generalized linear model with a Poisson distribution and log link function. I was told to use Poisson because I have count data with values ranging from a min of 1 to a max of 118 with most falling in the 5 to 50 range. The model shows 2 goodness of fit statistics (pearson, deviance) that both have p-values less than 0.05. Does this mean that the model results are invalid and I need to reanalyze using a different distribution? This blog below seems to indicate that the results of the deviance test alone are somewhat unreliable.
https://thestatsgeek.com/2014/04/26/deviance-goodness-of-fit-test-for-poisson-regression/
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of goodness of fit statistics in Poisson GLM
The whole model LRT is significant. The goodness of fit tests indicate lack of fit. Perhaps include an interaction term?
What do the diagnostic plots look like?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of goodness of fit statistics in Poisson GLM
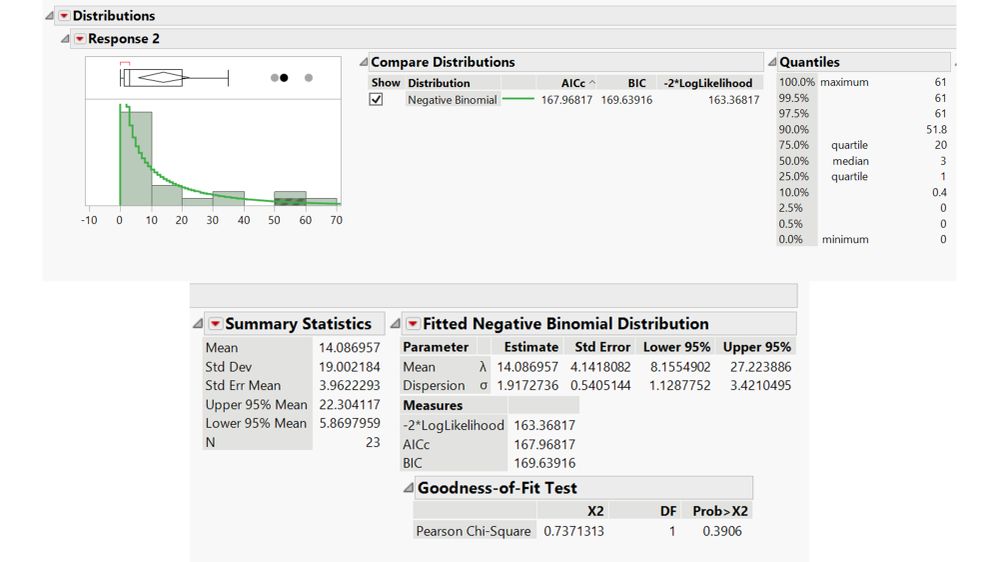
Thanks Mark. There were some over-dispersion issues, I believe, with the data. This morning I tried a negative binomial distribution and that fit seems much better.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of goodness of fit statistics in Poisson GLM
Did you invoke the over-dispersion option in the launch dialog when you fit the Poisson distribution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of goodness of fit statistics in Poisson GLM
I did not originally, but just tried it. The overdispersion value is 2.5197 (for Pearson). I've never used this option before so not sure how to interpret it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Use of goodness of fit statistics in Poisson GLM
The Poisson distribution uses a single parameter for the mean and the variance. As such, it might under-fit the data. The over-dispersion parameter allows for more variance than the mean.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us