- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- JMP > Identification of predictive signature from large data set > Issue with ob...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
JMP > Identification of predictive signature from large data set > Issue with obvious overfitting
Hi JMP community,
I have a large data set with ~4,000 biomarker measurements at Baseline in patients enrolled in a clinical trial. I need to identify among this data which combination of biomarkers may predict the clinical outcome 12 weeks later.
I have used a rather naive approach that appears to yield grossly overfitted outputs:
- Run all 4,000 biomarkers through the Screening > Response Screening where Response is the binary clinical output at week 12
- Select the top 10 - 20 biomarkers (based on FDR)
- Use the selected biomarkers (as Model Effects) on the Fit Model > Stepwise platform where Y is the binary clinical output at week 12; criteria = minimize BIC
- Generate the model
While this approach yielded excellent "predictors" to the clinical response at week 12 (ROC AUC > 0.940), it also yielded high ROC AUC when tested with a randomly generated "dummy" variable (ROC AUC ~0.870). The latter indicates to me that my method is grossly inappropriate because of overfitting.
I explored the feasibility of working with Discovery and Validation patient subgroups (50% of the entire population), but it did not solve my issue with overfitting.
Besides using the advanced modeling platforms provided by JMP Pro, are there better techniques in JMP to approach such a question?
Thank you for your help.
Best,
TS
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP > Identification of predictive signature from large data set > Issue with obvious overfitting
Thanks for the example. Let's look at closely, from a couple of perspectives. And they should lead to the same conclusion: there is no gold in the data.
First perspective, split data into training and validation, one should not attempt to use the fitted model based on the result from your script.
Second perspective, just fit the good and old logistic regression without train/val splitting, and see whether there are warning signs.
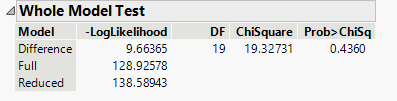
First warning sign: whole model test, which says there is great chance the model is no better than random guess.
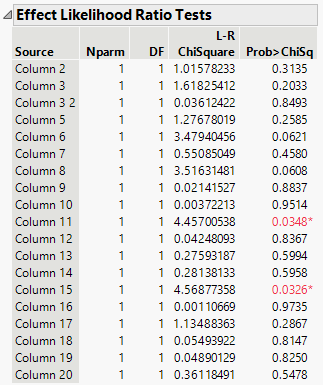
Second warning sign: Effect Tests and Parameter Significance. Here is Effect Tests. Only two reds. If those two are the gold, the rest are rubbles. Rubbles make us think they are gold. Remove them, shall we?
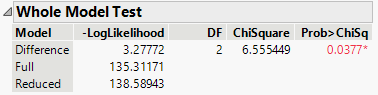
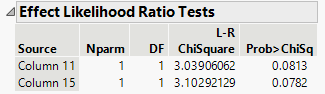
Ok, now what comes out from the other end of the sluice box is the following Whole Tests and Effect Tests. And pay attention to these p-values. They are around 0.05 and 0.10. On the fence, by usual means. Should we keep them? If we remove them, then we get random guess. Let's pretend that we really want to keep them, and see how it goes.
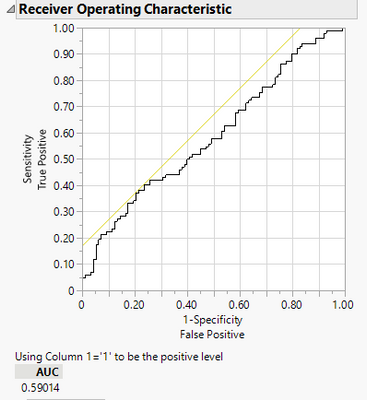
How about ROC and AUC?
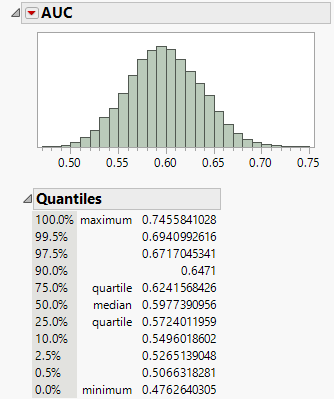
So AUC is 0.59. Gold? I guess that it is on the fence by usual means as well, because the model fitting says the model is on the fence, so should be everything derived from it. Need a proof? Yes, we can have a proof. We can bootstrap the AUC value, if you have JMP Pro. Right click on AUC value, and select Bootstrap. I gave it a 10000 draws. And 0.5 is within the range of the bootstrap samples. So it really comes down to how much one want to believe those two remaining factors are gold.
What I have done is to put a bootstrap confidence interval around AUC. We can make confidence intervals around ROC as well, so we may see the nice half shell is not that impressive at all. It would take a lot of effort to do so, though. Let's just look at one point ROC instead: the point corresponding to 0.5 cutoff threshold. Here are the steps.
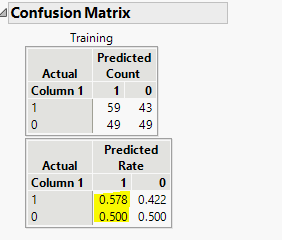
First, turn on Confusion Matrix.
Look at the highlighted numbers, they are True Positive Rate and False Positive Rate corresponding to the 0.5 cutoff threshold.
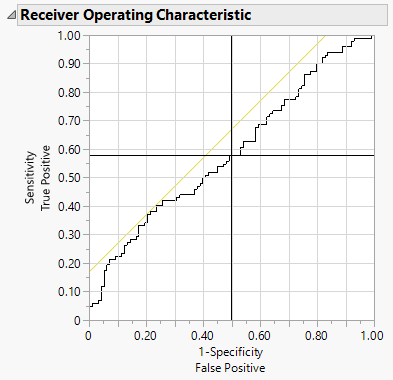
And we can find this point on ROC as in the following screenshot at the cross.
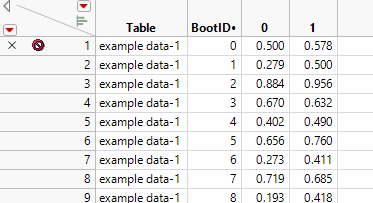
Now bootstrap those highlighted numbers. And I get this table, in which column "0" is bootstrapped False Positive Rate, and column "1" is bootstrapped True Positive Rate.
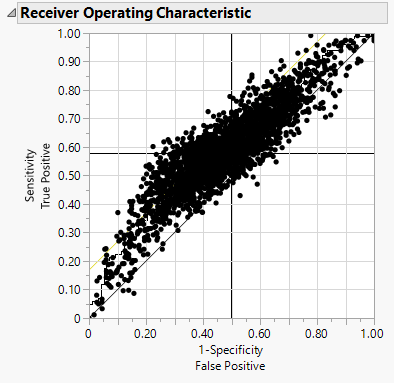
Plot column "1" vs column "0", and overlay on the ROC. And here is what I get. I also put a diagonal line as a reference.
What the bootstrap sample says that the probability 0.5 threshold point on ROC had a great chance over the diagonal line, but there is non-negligible chance below the diagonal. It is on the fence, if we should have concluded already from the model.
So what I want to conclude from this example is that we should really nail the model before concluding the model overfits. Including random noise as effects will overfit in this case.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP > Identification of predictive signature from large data set > Issue with obvious overfitting
Can you provide some more detail about your randomly generated response variable? How exactly did you create it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP > Identification of predictive signature from large data set > Issue with obvious overfitting
Hi Dale,
Thanks for following up on this relatively open question. I created the random variable using the following formula:
random uniform (0,1) > 0.5;Of note, I ran my "method" described above on eight different versions of the dummy variable (i.e., recalculate formula), yielding ROC AUC values ranging from 0.770 to 0.870.
I never came across such a behavior, but I have never worked with more than 1,200 biomarker variables.
Thanks for your help.
Best,
TS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP > Identification of predictive signature from large data set > Issue with obvious overfitting
I don't know the answer, but I can confirm what you found. I created a binary response variable (random) and 20 random normal factors with 200 observations. I got AUC=.71! I find it very surprising indeed. I suspect it has something to do with a limitation of the AUC as a performance measure, but as I said, I don't really understand this behavior. In my case, it certainly should not be overfitting. I'm anxious to see what others can say about this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP > Identification of predictive signature from large data set > Issue with obvious overfitting
To add to the mystery, I've attached the simulation I did. This time I used a validation column. Things worth noting: the logistic regression (script saved in the file) shows AUC around .71 for training data and much lower (less than .5) for the validation data. That is clear evidence of overfitting. However, I also ran the model screening - all the methods (including the logistic regression) show AUC around 0.5 for the training data and lower for the validation data - that seems reasonable to me. In addition, the logistic regression model is not significant (and only 1 or 2 factors are significant, about what you'd expect for 20 random factors). Among the things I don't understand is why the logistic regression platform and logistic regression within the model screening platform give such different results. I know (or believe) that model screening does not find tune hyperparameters as much as the individual modeling platforms, but the difference between 0.7 and 0.5 on the training data seems too large to me.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP > Identification of predictive signature from large data set > Issue with obvious overfitting
Thanks for the example. Let's look at closely, from a couple of perspectives. And they should lead to the same conclusion: there is no gold in the data.
First perspective, split data into training and validation, one should not attempt to use the fitted model based on the result from your script.
Second perspective, just fit the good and old logistic regression without train/val splitting, and see whether there are warning signs.
First warning sign: whole model test, which says there is great chance the model is no better than random guess.
Second warning sign: Effect Tests and Parameter Significance. Here is Effect Tests. Only two reds. If those two are the gold, the rest are rubbles. Rubbles make us think they are gold. Remove them, shall we?
Ok, now what comes out from the other end of the sluice box is the following Whole Tests and Effect Tests. And pay attention to these p-values. They are around 0.05 and 0.10. On the fence, by usual means. Should we keep them? If we remove them, then we get random guess. Let's pretend that we really want to keep them, and see how it goes.
How about ROC and AUC?
So AUC is 0.59. Gold? I guess that it is on the fence by usual means as well, because the model fitting says the model is on the fence, so should be everything derived from it. Need a proof? Yes, we can have a proof. We can bootstrap the AUC value, if you have JMP Pro. Right click on AUC value, and select Bootstrap. I gave it a 10000 draws. And 0.5 is within the range of the bootstrap samples. So it really comes down to how much one want to believe those two remaining factors are gold.
What I have done is to put a bootstrap confidence interval around AUC. We can make confidence intervals around ROC as well, so we may see the nice half shell is not that impressive at all. It would take a lot of effort to do so, though. Let's just look at one point ROC instead: the point corresponding to 0.5 cutoff threshold. Here are the steps.
First, turn on Confusion Matrix.
Look at the highlighted numbers, they are True Positive Rate and False Positive Rate corresponding to the 0.5 cutoff threshold.
And we can find this point on ROC as in the following screenshot at the cross.
Now bootstrap those highlighted numbers. And I get this table, in which column "0" is bootstrapped False Positive Rate, and column "1" is bootstrapped True Positive Rate.
Plot column "1" vs column "0", and overlay on the ROC. And here is what I get. I also put a diagonal line as a reference.
What the bootstrap sample says that the probability 0.5 threshold point on ROC had a great chance over the diagonal line, but there is non-negligible chance below the diagonal. It is on the fence, if we should have concluded already from the model.
So what I want to conclude from this example is that we should really nail the model before concluding the model overfits. Including random noise as effects will overfit in this case.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us