- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: JMP Pro > Dimension Reduction > PCA > Retrieve Most Meaningful Components?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
JMP Pro > Dimension Reduction > PCA > Retrieve Most Meaningful Components?
Hi,
I am working on a relatively large dataset that includes ~1,500 variables (i.e., biomarkers). Since subsets of these variables tend to correlate with each other, I wish to reduce the dimensions of the dataset. I am currently exploring PCA to achieve this goal. Still, I am unsure how to link back specific principal components with the original data (i.e., which biomarkers/variables contribute the "most" to the specific principal components). I know how to retrieve the Formatted Loading Matrix, but how can I set a meaningful cutoff for selecting the most influential components of the principal components?
Of note, the specific principal components of interest are derived from a simple linear model testing the association of each PC with a clinical variable.
Windows Pro
JMP Pro 16.1
Thank you for your help.
Best,
TS
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Pro > Dimension Reduction > PCA > Retrieve Most Meaningful Components?
Hi @Thierry_S,
There are perhaps some options interesting to consider for your use case :
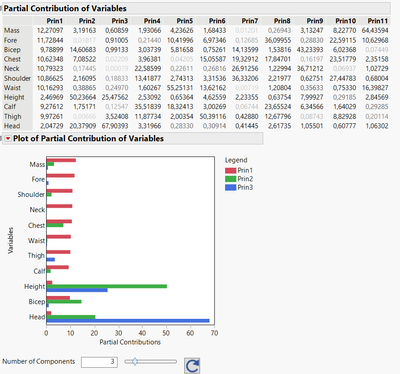
- Partial contribution of variables : In the red triangle of the PCA platform, you can select "Partial Contribution of Variables", which offers an interesting view on which variables are the most influent in which principal components, and the table provided before the plot is helpful to estimate these relative influences :
- Cluster Variables : Helps define non-overlapping clusters of variables and may help you select the most interesting/important contributing variables to the different clusters.
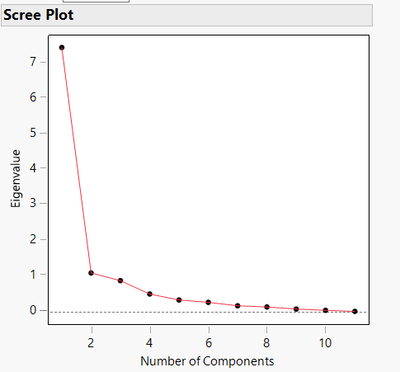
- Scree plot : Finally, if you want to estimate an appropriate number of principal components to use (good compromise between accuracy/variability explanation and complexity/number of PCs), the Scree plot is a very nice option, showing the eigenvalues depending on the principal components order :
Common approach in litterature recommends selecting only a number of PCs which provide eigenvalue >1 and not beyond the "elbow" region (as for each additional factor, the eigenvalue doesn't change a lot, meaning the contribution of each additional variable is not very high).
"Those with eigenvalues less than 1.0 are not considered to be stable. They account for less variability than does a single variable and are not retained in the analysis. In this sense, you end up with fewer factors than original number of variables. (Girden, 2001)" : https://stats.stackexchange.com/questions/72439/why-eigenvalues-are-greater-than-1-in-factor-analysi...
I hope these first options will help you,
Best,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Pro > Dimension Reduction > PCA > Retrieve Most Meaningful Components?
Hi @Thierry_S,
There are perhaps some options interesting to consider for your use case :
- Partial contribution of variables : In the red triangle of the PCA platform, you can select "Partial Contribution of Variables", which offers an interesting view on which variables are the most influent in which principal components, and the table provided before the plot is helpful to estimate these relative influences :
- Cluster Variables : Helps define non-overlapping clusters of variables and may help you select the most interesting/important contributing variables to the different clusters.
- Scree plot : Finally, if you want to estimate an appropriate number of principal components to use (good compromise between accuracy/variability explanation and complexity/number of PCs), the Scree plot is a very nice option, showing the eigenvalues depending on the principal components order :
Common approach in litterature recommends selecting only a number of PCs which provide eigenvalue >1 and not beyond the "elbow" region (as for each additional factor, the eigenvalue doesn't change a lot, meaning the contribution of each additional variable is not very high).
"Those with eigenvalues less than 1.0 are not considered to be stable. They account for less variability than does a single variable and are not retained in the analysis. In this sense, you end up with fewer factors than original number of variables. (Girden, 2001)" : https://stats.stackexchange.com/questions/72439/why-eigenvalues-are-greater-than-1-in-factor-analysi...
I hope these first options will help you,
Best,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Pro > Dimension Reduction > PCA > Retrieve Most Meaningful Components?
Your query is quite typical for practitioners. Pardon my over simplification.
The interpretation of Eigenvectors is not easily understood by the practitioner (by this I mean scientist or engineer). The eigenvectors are likely some combination (and subset) of the biomarkers in your study. Since eigenvectors are looking at the data through a different "dimension", that dimension may be non-sensical our have no intrinsic meaning from a practical standpoint. Eigenvectors don't have a familiar "name". Hopefully, what PCA will do is to identify the need and provide motivation for further investigation.
How did you get your data? Are the variations in any of the biomarkers biased (e.g., do some vary more than others)? If you already know some of the biomarkers are collinear (or correlated or redundant), can you use this knowledge to reduce the number of biomarkers before doing PCA?
Now, some folks don't really care to understand (what are these eigenvectors and how do they relate to the variables in my raw data?) and just want a model that "works" (perhaps like neural networks).
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us