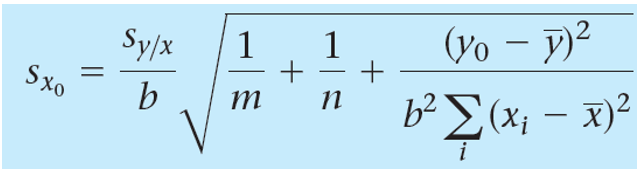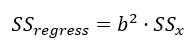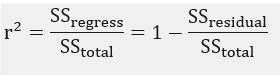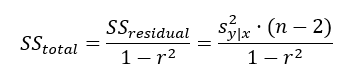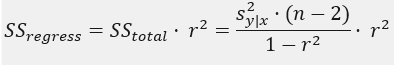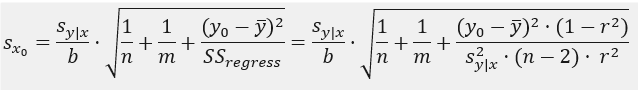- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Inverse prediction of sample with error in y
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Inverse prediction of sample with error in y
Hello,
I'm working with calibration curves (Using the add-in Calibration Curves - JMP User Community) and would like to output a CI for a measured value. I understand how to make use of the inverse prediction function, what I don't know how to do is how to incorporate multiple measurements (triplicates) into my analysis. In short, how do I account for the variability in Y when doing a "Y by X" inverse prediction?
Thanks,
BRP
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Inverse prediction of sample with error in y
I think the middle ground is achievable. But let me illustrate how the inverse prediction intervals for an individual response and the expected response are obtained.
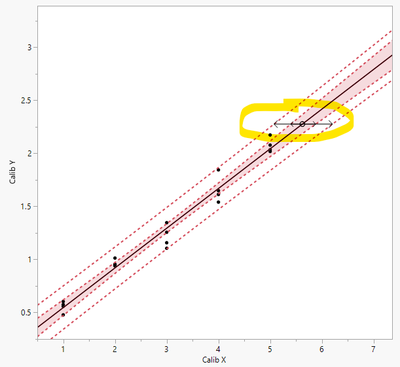
The following screenshot is obtained by copying the contents of two inverse prediction plots, and pasting into the fitted curve plot.
Look at how the ends of arrows touch the confidence interval bands and prediction interval bands.
So, the inverse prediction "uncertainty interval" is obtained by finding the intersections of the "y" value and desired "uncertainty bands".
Now, look at your middle ground. What is the definition of the "uncertainty bands" of your middle ground. It should be somewhere between the confidence interval bands and prediction interval bands.
Now you need some math. This is the related math in JMP documentation:
I put a screenshot below, and pay attention to the highlighted ONE!
For you middle ground, that should be 1/K, where K is the number of your replicates.
The formula above is for general regression. Even I tell you the solution, it might be difficult for you to calculate. But since your regression is simple, you might be able to do so. Check out the following page:
https://online.stat.psu.edu/stat501/lesson/3/3.3
And use the formula there to get the "uncertainty bands" of your middle ground. Then find out the intersection between the bands and a given "y", the average of replicates.
Update:
I want to add one more thing. You mentioned the measurements are "replicate" on the same entity, e.g. three measurements of height of the same person. In that case, the problem in your hands is not a simple regression. And the following book should be useful to you:
JMP for Mixed Models, by my colleagues: Ruth Hummel, Elizabeth Claassen, and Russell Wolfinger.
https://www.amazon.com/JMP-Mixed-Models-Ruth-Hummel/dp/195236521X
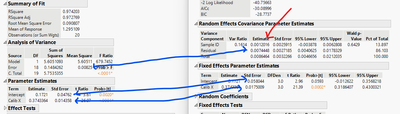
I attach the updated data, with a Fit Mixed script. Then look at the comparisons of results from Least Squares and Mixed:
The blue arrows point to quantities that have different estimates.
The red arrow points to the quantity of estimate of the variance of a single new "y".
Your "middle ground" is still achievable, but the complexity just went up.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Inverse prediction of sample with error in y
There are at least two distinct situations, which are not clear based on you description.
First situation, every Y is measured from a unique entity. I.e. Y's are independent. For this situation, you typically have one curve to model. For this situation, one plausible approach is to study the confidence interval of Y given X, and vice versa. The latter is the inverse prediction that you are interested. One method is literally done by finding the intersections of the upper and lower confidence bands of Y given X, with the horizontal threshold.
Second situation, every entity has multiple measurements over different X's. By such, some Y's are independent, some are not. For this situation, you have multiple curves to model, one curve for each entity. For this situation, you may or may not be able to derive the distribution of the crossing points of the curves. But if you can simulate these curves, simulate them, calculate the intersections, and find the quantities of interest.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Inverse prediction of sample with error in y
So it's basically analyzing the same sample 3 times, which should give the same X, and I believe describes your first method. If I understand you correctly, you'd take calculate the predicted x from the y average, and the x interval as the 95% individual confidence of both the low and the high y CI?
Or an alternative way to ask the question I suppose, how does the "individual confidence region" change for a group of replicate measures?
Is there any way to build that into the report or would I have to go to a script? Similarly, any easy way to get around the limit of 8 values in the inverse prediction? Can I inverse a whole column in my data table?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Inverse prediction of sample with error in y
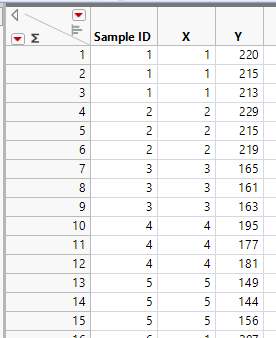
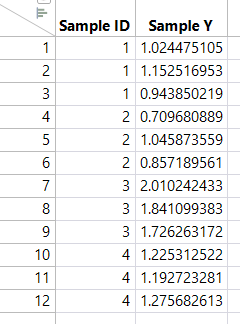
I think I am on the path of better understanding about this. I attach a simulated data.
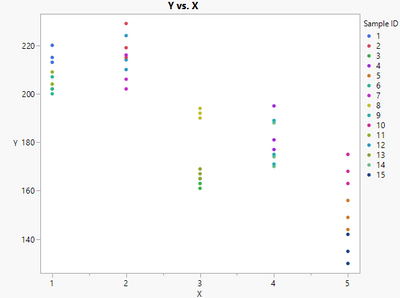
It looks like this. It has 15 distinct Sample ID, which means there are 15 distinct entities that you measure. X is where you measure. There are 5 levels, 1 through 5. And Y is the measurement. Each entity has 3 measurements.
And there is a script in the data table, which produces this plot
You would like to fit a line, and you are interested in the confidence interval of the inverse prediction using the fitted line. Am I understanding correctly?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Inverse prediction of sample with error in y
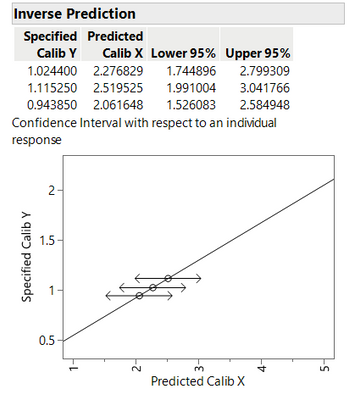
Almost- I think JMP already provides a confidence interval based on the error of the fit curve, that's what the typical inverse prediction does, right?
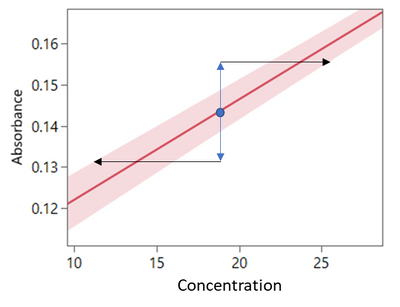
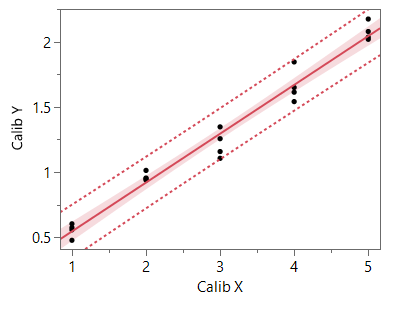
I want to, for a given calibration curve: (shaded is fit, dotted is individual confidences)
Get an estimate of the inverse prediction error when I have sampled a single (non calibration) entity several times.
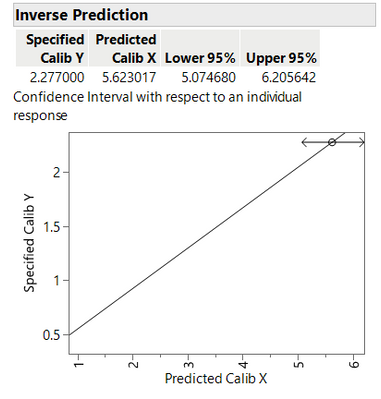
Currently I can make an inverse prediction with respect to an individual response (which I assume is a single measurement)
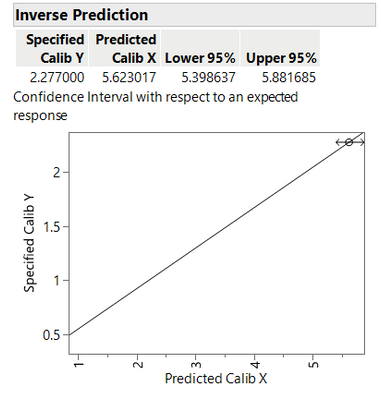
Or with respect to an expected response, which I believe assumed your measurement is "correct" and only accounts for the uncertainty in the calibration.
I'd like to find the middle ground, where I can specify an average response and variance for a sample group of n = 3, or any other replicate
Alternatively, is it possible (or even correct?) to combine the three individual estimates somehow?
Simulated data attached - Thanks again
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Inverse prediction of sample with error in y
I think the middle ground is achievable. But let me illustrate how the inverse prediction intervals for an individual response and the expected response are obtained.
The following screenshot is obtained by copying the contents of two inverse prediction plots, and pasting into the fitted curve plot.
Look at how the ends of arrows touch the confidence interval bands and prediction interval bands.
So, the inverse prediction "uncertainty interval" is obtained by finding the intersections of the "y" value and desired "uncertainty bands".
Now, look at your middle ground. What is the definition of the "uncertainty bands" of your middle ground. It should be somewhere between the confidence interval bands and prediction interval bands.
Now you need some math. This is the related math in JMP documentation:
I put a screenshot below, and pay attention to the highlighted ONE!
For you middle ground, that should be 1/K, where K is the number of your replicates.
The formula above is for general regression. Even I tell you the solution, it might be difficult for you to calculate. But since your regression is simple, you might be able to do so. Check out the following page:
https://online.stat.psu.edu/stat501/lesson/3/3.3
And use the formula there to get the "uncertainty bands" of your middle ground. Then find out the intersection between the bands and a given "y", the average of replicates.
Update:
I want to add one more thing. You mentioned the measurements are "replicate" on the same entity, e.g. three measurements of height of the same person. In that case, the problem in your hands is not a simple regression. And the following book should be useful to you:
JMP for Mixed Models, by my colleagues: Ruth Hummel, Elizabeth Claassen, and Russell Wolfinger.
https://www.amazon.com/JMP-Mixed-Models-Ruth-Hummel/dp/195236521X
I attach the updated data, with a Fit Mixed script. Then look at the comparisons of results from Least Squares and Mixed:
The blue arrows point to quantities that have different estimates.
The red arrow points to the quantity of estimate of the variance of a single new "y".
Your "middle ground" is still achievable, but the complexity just went up.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Inverse prediction of sample with error in y
Not as simple a solution as I was hoping for - but perfect answer. I appreciate the explanation of the CI derivations. I may write myself a little script/module to do this calculation in the future. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Inverse prediction of sample with error in y
According to Statistics and Chemometrics for Analytical Chemistry, Mille & Miller, 7th edition, the std. error on the x-axis 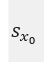
where
If you use the add-in calibration curve https://community.jmp.com/t5/JMP-Add-Ins/Calibration-Curves/ta-p/22095
you get the necessary information to make the calculation of post the analyses in a new separate table.
The output table consist of these columns:
By Group | RSquare | RSquare Adj | Root Mean Square Error | Mean of Response | Observations (or Sum Wgts) | Intercept | Conc. |
In simple linear regression the regression coefficient is defined as:
Thus
and therefore
It follows that
Thus if you define a few new columns including with m and 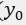
I enclose an example for your reference.
I lack expertise in JSL but it would be nice if these option where added to the calibration curve add-In script.
Hope this help.
/Flemming
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us