Interpreting three-way anova: Effects test of interaction not significant but post hoc seems significantly different

[#1]

Hi,

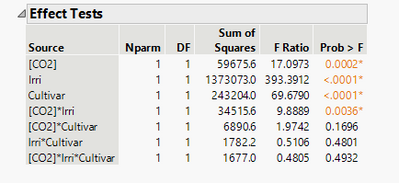
I performed a three-way anova to see the effects of factors(CO2, irrigation and cultivar) on the wheat grain numbers.

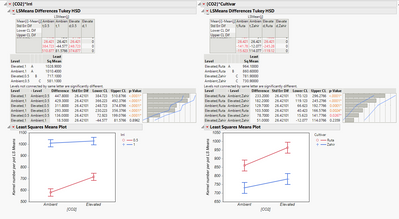
Effects shown that the interaction of CO2 and Cultivar was not significant(p>0.05), but the Tukey test seems there is the interaction between them.

When I look into the interaction of CO2 and irrigation, they  looks similar to the interaction of CO2 and cultivar, but the effects test of which was actually significant.

I did not understand why the multiple comparison show there is interaction but the effect test tells me no.

[#2]

You can get different answers because these tests are asking two different questions. The effect test is asking if the term, as a whole, changes the model significantly when it is added along with the other terms. It is based on the sum of squares associated with adding the term. There might not be sufficient evidence (mean square) to indicate a significant term (F ratio). The Tukey test, on the other hand, is asking about differences between in the least squares means of combinations of factor levels. So it is possible that the test for the whole term is not significant but differences between some combinations of factor levels are significant. They often agree, but there is actually no requirement that they should.

[#3]

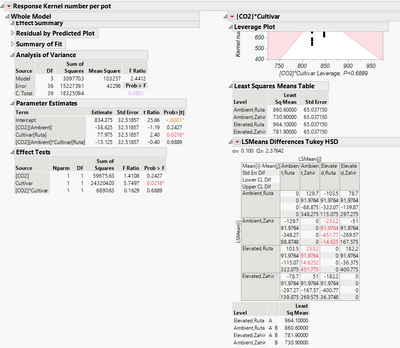
When doing a 2-way ANOVA (not considering irrigation effect), I see that the interaction effect of the above is not significant, likewise a turkey test on the interaction term. I can't possibly understand why we have a difference when doing the 3-way ANOVA (as above). In such a situation where I need to consider all terms (main factors), what do I or rather how do I represent such discrepancy. Can you help with guidance here?

[#4]

First of all, I explained that the overall ANOVA and the individual effect tests are based on adding a set of terms or a term, respectively, and are not a statement about any pair of levels. The Tukey comparisons, on the other hand, are about the levels. Even though Tukey adjusts for the number of comparisons so that the type I error rate is experiment-wise instead of comparison-wise, it is still (apparently) 0.05 so when you make enough tests like your example so far, you are likely to get a false positive.

It also seems that you are trying lots of different comparisons. Your experimental design is inadequate to support so many tests. The design assumes that you are making specific inferences. Be careful to avoid "cherry picking" until you get a positive result.

In either case, if you believe the comparisons found by the Tukey method, then you need to confirm them with new, independent observations.

Finally, before statman gets a chance to ask, are the differences meaningful or practically important, regardless of the statistical significance?

[#5]

Had to laugh...spit my beer out.  How right you are.

[#6]

  ... so Statman what do you say??

[#7]

Usually, and if I understand clearly if the null hypothesis is accepted it means that there are no differences between the means, so no need to do a post-hoc test or to expect any difference between groups as we see in my first question. How do we explain this?

[#8]

I'm not sure what you are asking me?  I think mark explained the difference in tests quite well.  What I recommend is to set the statistical tests aside for a moment.  Plot the data.  Evaluate the practical significance of the variation in the data.  Investigate the data for any unusual data points (this can be aided by predicting the results á priori ).  Often higher order effects are assigned when it is actually a "special cause"" data point.  Analysis should always follow the sequence: Practical, graphical then quantitative.