- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: How to reconcile prediction profiler confidence intervals with parameter est...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
I have an mixture experiment with four components. It's a custom design of 16 runs with no replication that started with a model that included interactions of two factors and three components. The mixture constraint is that the four components sum to 1.0. The reduced model from the data has only the four main effects as statistically significant (p<.0001).
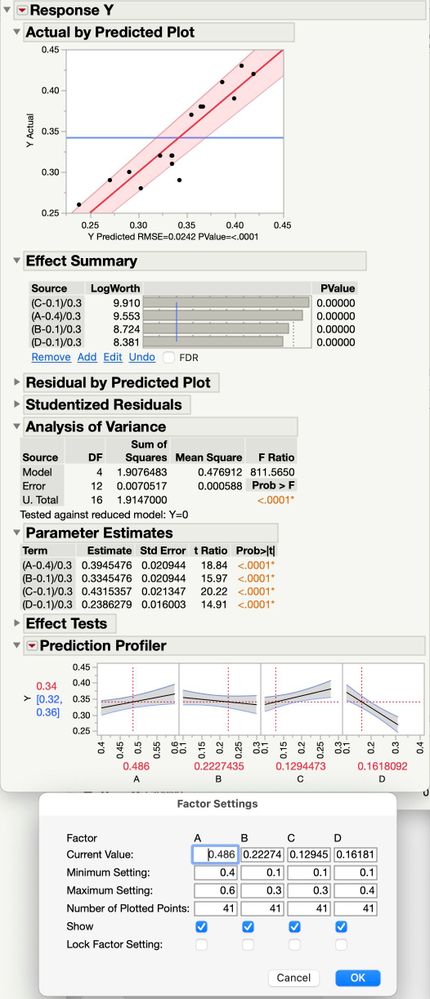
The prediction profiler plots show 95% confidence intervals that imply the "slope" of the effect of some significant factors could be zero; the gray band encompasses a horizontal line. It also shows the factor having the smallest effect has the largest slope.
The profiler also shows the slope of the effect of component A changing as I change the amount of component C, even though there are no interactions in the model. A has a slope of 0.05 units when C is at 0.1 and it has a slope of 0.02 units when C is 0.2. Of course the amounts of the other components change to stay within the inference space, but why the change in slope?
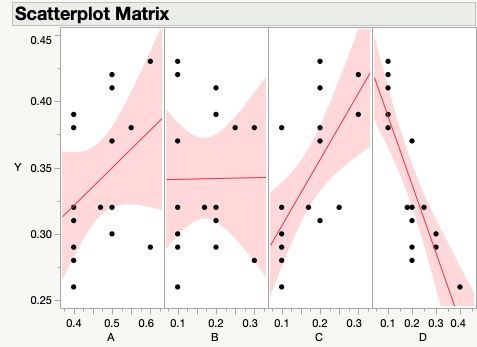
The attached graphic shows what I'm seeing. It also shows a Factor Settings dialog that has the min and max settings that were used in the mixture experiment.
The scatterplots and the prediction profiler plots looks similar, they make it look like factor B is insignificant. But if I leave B out of the model, the residual errors show that to be a mistake.
How do I interpret the slope and confidence intervals on the prediction profiler for this situation? Or maybe how do I relate the parameter estimates to the prediction profiler?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
The prediction profiler is showing you the profile of a component when all other components are fixed at the stated level (where the red vertical line is). If you drag one of the component settings, the others will need to move because of the mixture constraint. They will move in the same ratio that they are currently in. So, using that simple example data, the default prediction profiler is at the centroid (1/3, 1/3, 1/3). Moving one of the component settings will cause the other two to move in the opposite direction, but they will always be equal since they started off as equal. From the overall centroid, this would be like moving along the component axis. If you started with (1/6, 2/6, 3/6) -- yes, I could have simplified the fractions but left them this way to easily see the relationships -- and moved the third component, the first two would stay in the 1:2 ratio. This will always be true unless one of the components hits a boundary or limit. Then the profiler would run along that boundary, if necessary.
The mixture profiler actually shows you a surface for three components. Since you have four components, it will show you the surface with the fourth component fixed at whatever value you choose. Notice that above the profiler you can set all four components. For four components you have a 3-dimensional simplex design space. Fixing that fourth component has JMP show you the 2-dimensional surface for that slice in the 3rd dimension.
So to determine which components have the biggest impact, look at the slopes of the prediction profile. You will see that the response is more sensitive when that component is changed. Be careful of the cause-effect conclusions though. Remember, changing one component necessarily changes all of the others. So is a better response achieved because you raised component D? Or was it because you lowered all other components? The correct answer is BOTH!
Unfortunately, you cannot really test the parameter estimates to be equal to the mean. That test is not able to be accomplished because of the linear constraint. Although you can mentally think of such a test, the problem is that you are cheating. You would not know what the mean is until you estimate it from the data. Once you estimate it, you really can't claim that it is a known, fixed quantity. That is why JMP does not provide that test. In fact, in version 17 of JMP, the labeling on the mixture main effects is changed:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
It looks like the problem is that you are not analyzing the data with a Scheffe mixture model. Look at the Analysis of Variance table. You will see a message there that says "Tested against reduced model: Y=0". That means you are fitting a no-intercept model. What you SHOULD see for a mixture model is "Tested against reduced model: Y=mean".
So, what went wrong? Most likely someone did some rounding when entering the values of your four components. Create a column that is the sum of your four components and you will likely see something that is different than 1. The sum must be 1 EXACTLY for JMP to analyze the data as a mixture. Once that is fixed, try re-fitting the model. Come back here if you still have questions at that point.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
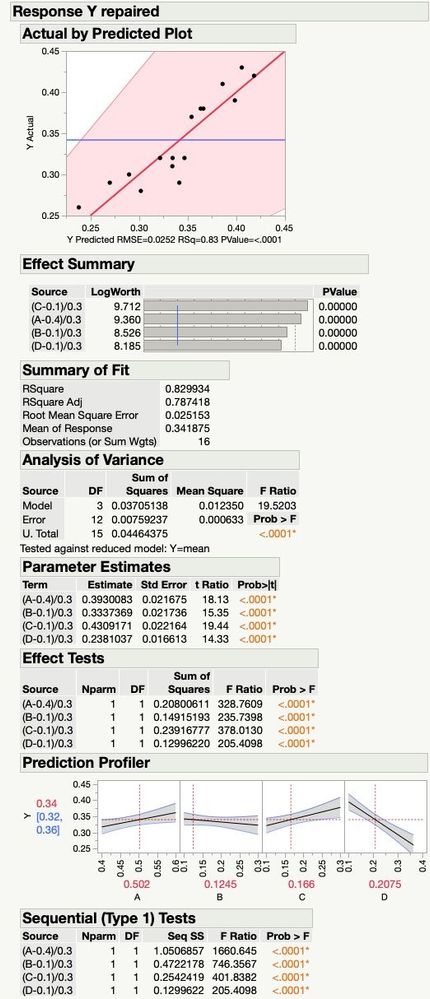
Thanks Dan, it turns out that one of the rows did not sum to 1.0. When I repaired it (changed one proportion from 0.47 to 0.48), then the result made me more confused.
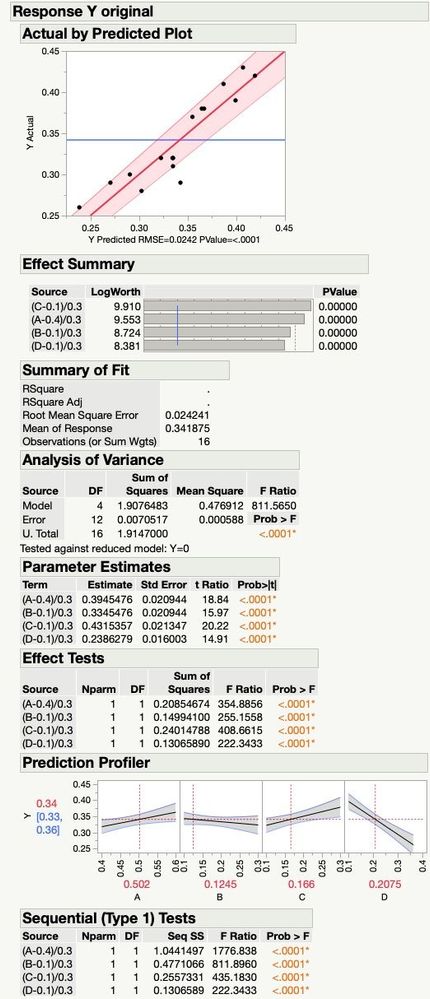
The sums of squares (sequential and adjusted) changed hardly at all, including the error SS in the ANOVA. But, Model SS in ANOVA is nowhere near the same. The total sums of squares for the sequential SS don't sum to the value in the ANOVA in the repaired analysis like they did in the original. Somehow 1.87 units of SS have gone somewhere that I don't see.
The confidence intervals in the response profiler are the same, but not in the Y Actual by Y Predicted plot. The parameter estimates are nearly unchanged.
The attached images show the differences, one is entitled "Response Y original" the other is "Response Y repaired". You can see that the message in the ANOVA table is either "Y=0" or "Y=mean".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
You will only need to be concerned with your Y repaired.
The Scheffe mixture model cannot be interpreted like a typical regression model. It looks like there is no intercept in the model, but there is. The intercept is included with the main effects. The interpretation is what matters. For example, the main effect parameter estimates are actually the height of the response surface at the pure component vertex of the respective components. In other words, it is the "effect" of the component plus the overall mean. That is why the ANOVA has the message "Tested against Y=mean". So the type I SS will not add up properly because of the mean being involved in all of the SS of the main effects.
The confidence bands on the observed versus predicted plot are correct for the Scheffe model. They are much wider because of the inherent multicollinearity caused by a mixture. When factors are correlated (as they are in a mixture), that leads to an inflation in the variance of the parameters. Thus, the error bands will be much wider on the model fit. The prediction profiler will look better because that is a confidence interval on the prediction, not the significance of the parameters.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
I'm starting to understand, I get that the model scales the value of the component in such a way that there is effectively an intercept. However, it also appears that the sensitivity of the model to a component is proportional to the parameter estimate. I suppose I need to find some papers that describe the statistics of the significance for Scheffe models.
There is a JMP Help somewhere that says the confidence interval on the Prediction Profiler is confidence on the mean, not on an individual prediction. If it's not related to significance of the parameters, or to the sensitivity of the model to changes in the component, what is the utility of confidence intervals on the Prediction Profiler?
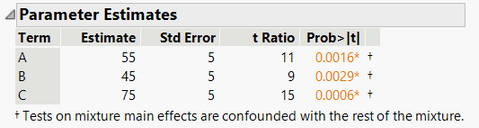
What is the slope on the prediction profiler trying to convey? Why is the slope for component D greater than any of the others, but its parameter estimate is the smallest? Why do the slopes of A and B look insignificant but their parameter estimates are larger than D?
I suppose what I need is a Methods and Formulas reference for this platform and I can work it out from there. The math behind the scenes is a little opaque.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
Essentially, a Scheffe mixture model is a constrained regression. That is what throws off all of the regular statistics. The main component parameter estimates are constrained by the overall average of the data.
The Scheffe model for three components was created in this fashion:
For three components, a typical regression model would be y=b0 + b1x1 + b2x2 + b3x3. A design to estimate this model (for an unconstrained case) would be the three experiments that are pure component runs. (1, 0, 0), (0, 1, 0), and (0, 0, 1). But I have four parameters in the model. You cannot estimate four things with three trials. So, we rewrite the model as y = b0(x1+x2+x3) + b1x1 +b2x2 + b3x3. Essentially, just rewriting the intercept as b0 times a funny looking one. Multiplying out and regrouping gives the familiar Scheffe form: y = b1*x1 + b2*x2 + b3*x3. The stars indicate that they would be the original coefficients plus b0.
Because of the constraint, if a component has "no effect" (whatever that means in a mixture situation), then the parameter estimate would be the same as the overall mean. The response does not change along that axis of the mixture simplex. For this reason, component D has the largest effect. That parameter estimate of 0.2381 is the FURTHEST AWAY from the overall mean of the data 0.341875.
Although the profiler is helpful, you might also want to consider the Mixture Profiler that is available under the red triangle. That may help.
As for reading more about Scheffe models, the bible of mixture experimentation is the book Experiments with Mixtures by John Cornell. Very good book that goes into much more detail on how the Scheffe model was created, how to interpret it, and how to design mixture experiments to estimate such a model. It also discusses alternative mixture models, as the Scheffe model is just one approach to handle the mixture constraint.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
I think a simple example might help you see the model better. I have attached the file with a script for some output from the model. Pay particular attention to the response values and what the corresponding parameter estimate is. You should notice the pattern. Also notice that the parameter estimates significant test declares the three components as significant because it is testing against 0. That test is not really meaningful, as indicated by what you will see on the prediction profiler.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
Dan, thanks this simple example is helpful. It's clear that testing against zero and testing against the mean are critical.
What's not clear is how to answer the question of which components have large or small sensitivities. Maybe for my example the prediction profiler is answering that graphically by showing B is nearly horizontal.
It appears that the prediction profiler is taking a slice through the response surface. It's not clear where the slice lies, meaning how the A, C and D will track as the red line is moved on B. What's the principle of operation for that and for the mixture profiler?
Is there a way to test the hypothesis that a parameter is equal to the mean? Do it manually?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
The prediction profiler is showing you the profile of a component when all other components are fixed at the stated level (where the red vertical line is). If you drag one of the component settings, the others will need to move because of the mixture constraint. They will move in the same ratio that they are currently in. So, using that simple example data, the default prediction profiler is at the centroid (1/3, 1/3, 1/3). Moving one of the component settings will cause the other two to move in the opposite direction, but they will always be equal since they started off as equal. From the overall centroid, this would be like moving along the component axis. If you started with (1/6, 2/6, 3/6) -- yes, I could have simplified the fractions but left them this way to easily see the relationships -- and moved the third component, the first two would stay in the 1:2 ratio. This will always be true unless one of the components hits a boundary or limit. Then the profiler would run along that boundary, if necessary.
The mixture profiler actually shows you a surface for three components. Since you have four components, it will show you the surface with the fourth component fixed at whatever value you choose. Notice that above the profiler you can set all four components. For four components you have a 3-dimensional simplex design space. Fixing that fourth component has JMP show you the 2-dimensional surface for that slice in the 3rd dimension.
So to determine which components have the biggest impact, look at the slopes of the prediction profile. You will see that the response is more sensitive when that component is changed. Be careful of the cause-effect conclusions though. Remember, changing one component necessarily changes all of the others. So is a better response achieved because you raised component D? Or was it because you lowered all other components? The correct answer is BOTH!
Unfortunately, you cannot really test the parameter estimates to be equal to the mean. That test is not able to be accomplished because of the linear constraint. Although you can mentally think of such a test, the problem is that you are cheating. You would not know what the mean is until you estimate it from the data. Once you estimate it, you really can't claim that it is a known, fixed quantity. That is why JMP does not provide that test. In fact, in version 17 of JMP, the labeling on the mixture main effects is changed:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to reconcile prediction profiler confidence intervals with parameter estimates for mixture design
This is fascinating. It's all fitting together now. I'm glad to know that the trace of the profile is the slice through the response surface along a track where the other components are held at a constant ratio until a boundary is hit.
On your recommendation I've ordered the book Experiments with Mixtures by John Cornell from Amazon but it'll take a couple weeks to arrive. It's always good to go back to the source.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us