- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How to analyze the weather pattern data?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to analyze the weather pattern data?
I wanted to know whether due to climate change, the precipitation in the last 16 years (2004 to 2019) had changed from the previous 15 years (1989 to 2003). Our hypothesis is that the weather patterns has changed and precipitation in the last 16 years had increased.
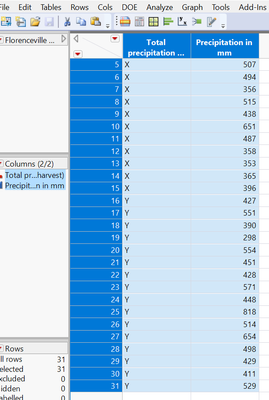
Here is the annual average data for different years.
|
Year |
Precipitation (mm) |
|
1989 |
384 |
|
1990 |
446 |
|
1991 |
471 |
|
1992 |
491 |
|
1993 |
507 |
|
1994 |
494 |
|
1995 |
356 |
|
1996 |
515 |
|
1997 |
438 |
|
1998 |
651 |
|
1999 |
487 |
|
2000 |
358 |
|
2001 |
353 |
|
2002 |
365 |
|
2003 |
396 |
|
2004 |
427 |
|
2005 |
551 |
|
2006 |
390 |
|
2007 |
298 |
|
2008 |
554 |
|
2009 |
451 |
|
2010 |
428 |
|
2011 |
571 |
|
2012 |
448 |
|
2013 |
818 |
|
2014 |
514 |
|
2015 |
654 |
|
2016 |
498 |
|
2017 |
429 |
|
2018 |
411 |
|
2019 |
529 |
I run this data using JMP after representing previous 15 years by X and last 16 years by Y. see below.
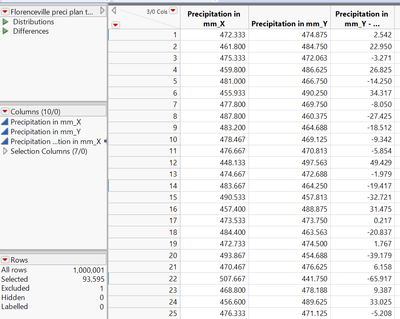
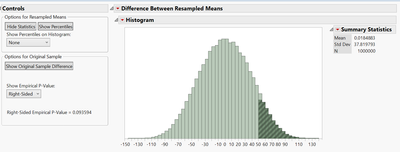
I performed permutation test. See below:
Results show that 91 per cent time I could say that the precipitation increased in the last 16 years (2004 to 2020) than previous 15 years (1989 to 2003).
My questions are as follows:
- Is the analysis correct?
- Should permutation performed with or without replacement?
- Is there any other method, which can give us better results for this kind of analysis for example “the linear trend model?”
Other questions:
When a frequency data ranges from 0 to 30 and there are so many zeros in data, should the data be transformed? Like taking the square root of each number, taking logarithm of each number (+.5) before fitting a “regression test” or “permutation test”?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to analyze the weather pattern data?
Hi,
I don't know anything much about permutation analysis so I can't answer those questions.
But there are other things you could do.
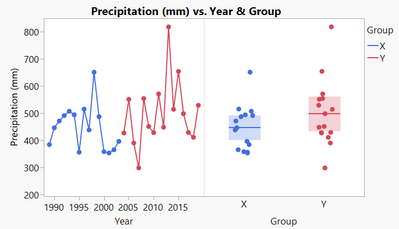
Start with simple plots of the data...
...there does not appear to be a big change between these periods.
I have attached a jmp data table with your data including scripts for this plot and Fit Y by X analysis (again, no evidence for a difference between these periods).
I also used Lasso in Generalized Regression for change points analysis (JMP Pro only). This suggested a change point between 2010-2011. @clay_barker has shown how to do this kind of thing before: https://community.jmp.com/t5/JMP-Blog/Did-LeBron-James-step-up-his-game-in-the-playoffs/ba-p/30609
I hope this helps.
Phil
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us