- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Bezier interpolation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Bezier interpolation
Hi,
Is there a function to plot Bezier interpolation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
Multiple answers, depending what you need to do. Here are some.
For 2D graphs you can use the path function. You can't find it by searching for Bezier because the scripting index spells it Bézier. Try searching for zier instead. @XanGregg @sheila_loring
This example extends the scripting index example with dragable handles.
// initial data; points 3 and 5 are not initially constrained about point 4
points = [
10 10 1,// move-to
30 70 0,// control point
40 10 0,// control point
50 40 3,// bezier
60 60 0,// control point
70 20 0,// control point
90 10 3 // bezier
];
// moving a square handle will call this function to
// copy the handle coordinates to the matrix
setpoint = Function( {index, x, y}, // parameters
{angle, distance}, // local variables
// copy to the matrix
points[index, 1] = x;
points[index, 2] = y;
// 3 and 5 are constrained about 4, comment out to see why...
// if the angles don't match, it isn't smooth
If( index == 3 | index == 5,
other = If( index == 3, 5, 3 ); // if I'm 3, he must be 5, etc
// trig in radians, 2*pi is 360
// atan does all 4 quadrants with 2 arguments
angle = ATan( points[index, 2] - points[4, 2], points[index, 1] - points[4, 1] );
// maintain other's distance
distance = Sqrt( (points[other, 2] - points[4, 2]) ^ 2 + (points[other, 1] - points[4, 1]) ^ 2 );
// fix other's angle to match my angle, but opposite me
points[other, 1] = points[4, 1] + distance * Cos( angle + Pi() );
points[other, 2] = points[4, 2] + distance * Sin( angle + Pi() );
);
// redraw
gb << inval;
);
New Window( "Example",
gb = Graph Box(
Fill Color( "blue" );
// there is no good shortcut for creating handles; the JSL holds the instances
Handle( points[1, 1], points[1, 2], setpoint( 1, x, y ) );
Handle( points[2, 1], points[2, 2], setpoint( 2, x, y ) );
Handle( points[3, 1], points[3, 2], setpoint( 3, x, y ) );
Handle( points[4, 1], points[4, 2], setpoint( 4, x, y ) );
Handle( points[5, 1], points[5, 2], setpoint( 5, x, y ) );
Handle( points[6, 1], points[6, 2], setpoint( 6, x, y ) );
Handle( points[7, 1], points[7, 2], setpoint( 7, x, y ) );
// construction lines
Pen Color( "red" );
Line( {points[1, 1], points[1, 2]}, {points[2, 1], points[2, 2]} );
Line( {points[3, 1], points[3, 2]}, {points[4, 1], points[4, 2]} );
Line( {points[4, 1], points[4, 2]}, {points[5, 1], points[5, 2]} );
Line( {points[6, 1], points[6, 2]}, {points[7, 1], points[7, 2]} );
// the bezier
Pen Color( "black" );
Path( points );
)
);I realized I should also constrain moving point 4 to drag points 3 and 5 along as well. (Not done, should be easy.)
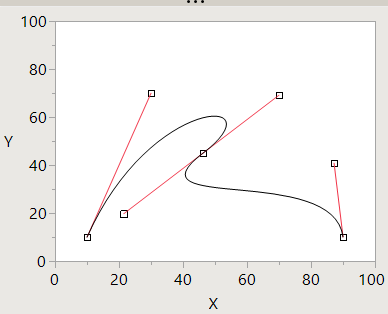
Maybe you need a spline. I'm not sure what the distinction between spline, p-spline, b-spline in the scripting index is. I used spline HeatColor vs Spline vs Interpolate to make this curve
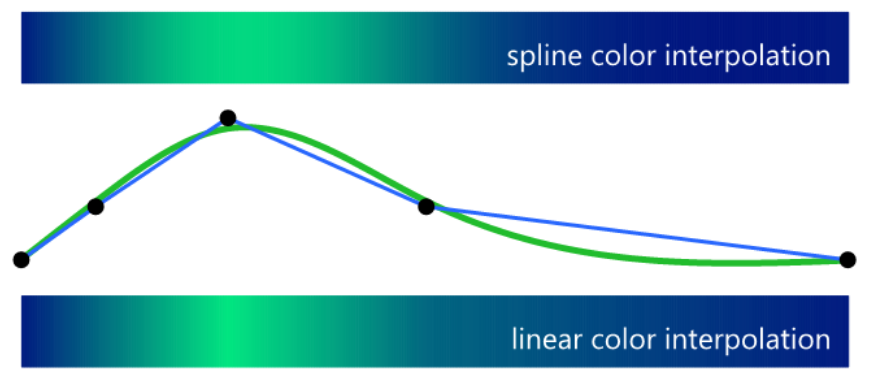
There is also support for Bezier splines in JMP's 3D OpenGL support: https://www.jmp.com/support/help/14-2/bezier-curves.shtml which might help draw a surface. A poor example is hidden in FFT Video
Great post @Duane_Hayes Understanding cubic splines
Something I ran into along the way: https://www.tinaja.com/glib/bezconn.pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
Hi Craige,
I am trying to understand path () function and move points, control points, bezier points.
I have these four points from the data I have
point =
[ 0.93 77.04 1,
1.37 155.22 0,
1.96 390.46 0,
2.41 846.87 3];
When I put this in path function, I get a line between point 1 and point 4, but it doesn't go through point 2 and point 3. Am I missing something?
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
What are you trying to do?
The wikipedia article is pretty good. The control points generally do not lie on the Bezier curve.
JMP can fit a spline to a set of points and gives you a slider to set the stiffness of the spline.
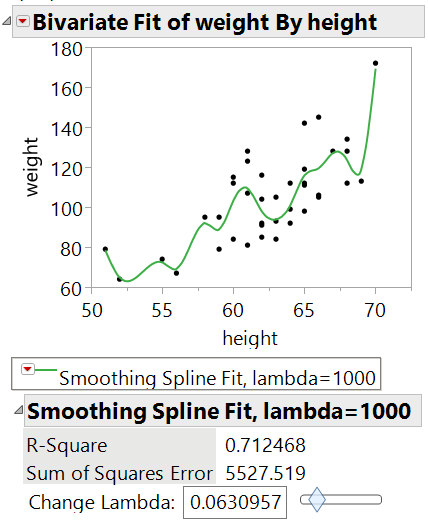
Edit: bad caption! NOT very stiff!
also see How to see equation used for spline? and cubic spline regression and How is the Smooth Line in the Graph Builder determined
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
This is what I am trying to do
Replicate Excel's scatter plot with a smooth curve feature.
If I use JMP fit Y by X with a flexible spine, I have a different curve than what Excel is producing with scatter plot + smooth line. I believe Excel is using Bezier curve fit.
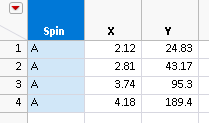
Datapoints:
Spin | X | Y
A | 2.41 | 846.8692
A | 0.93 | 77.043
A | 1.37 | 155.2193
A | 1.96 | 390.4639
I do not want to draw this line by using flexible spline, but I want to force bezier curve. I hope that makes sense.
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
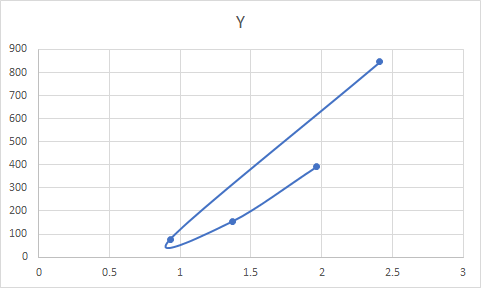
It would help if you appended the Excel chart you expect.
If I use the data (series) you provided, without sorting it, Excel creates the first graph below. If I sort the series in Excel, the second graph is teh result.
Note, that
- JMP platforms, by default fit a curve to the the data by value not by order in the table.
- Fit Y by X, fit Flexible, Kernel Smoother Linear Tri-Cube, would be the option I would use instead a spline, assuming you want a plot like the second plot below.
- To produce a plot like the first chart below where the curve accounts for the data order, you will need to create a script for a Path, as @Craige_Hales mentioned previously.
From your repsonse, it was not clear to me what you are looking for.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
Thinking about @gzmorgan0 explanation, you can do it in graph builder:
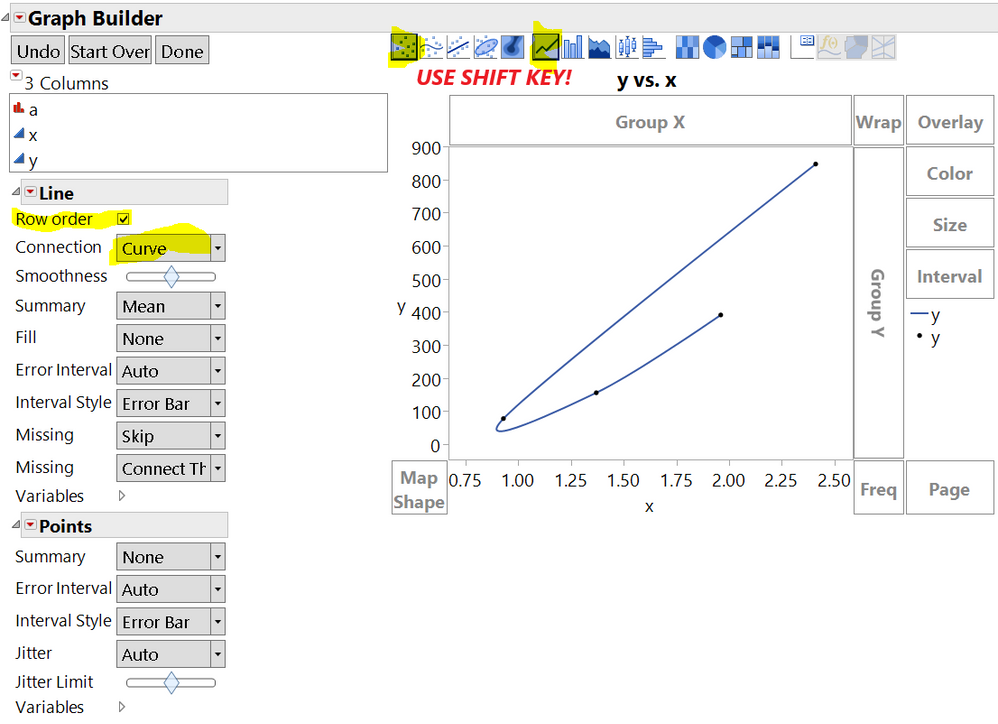
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
I apologize for the confusion here.
Data:
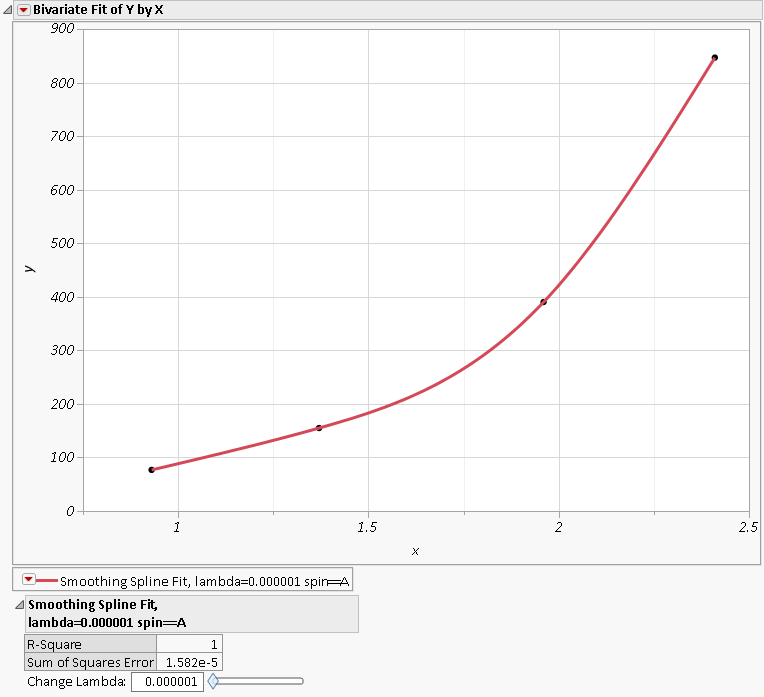
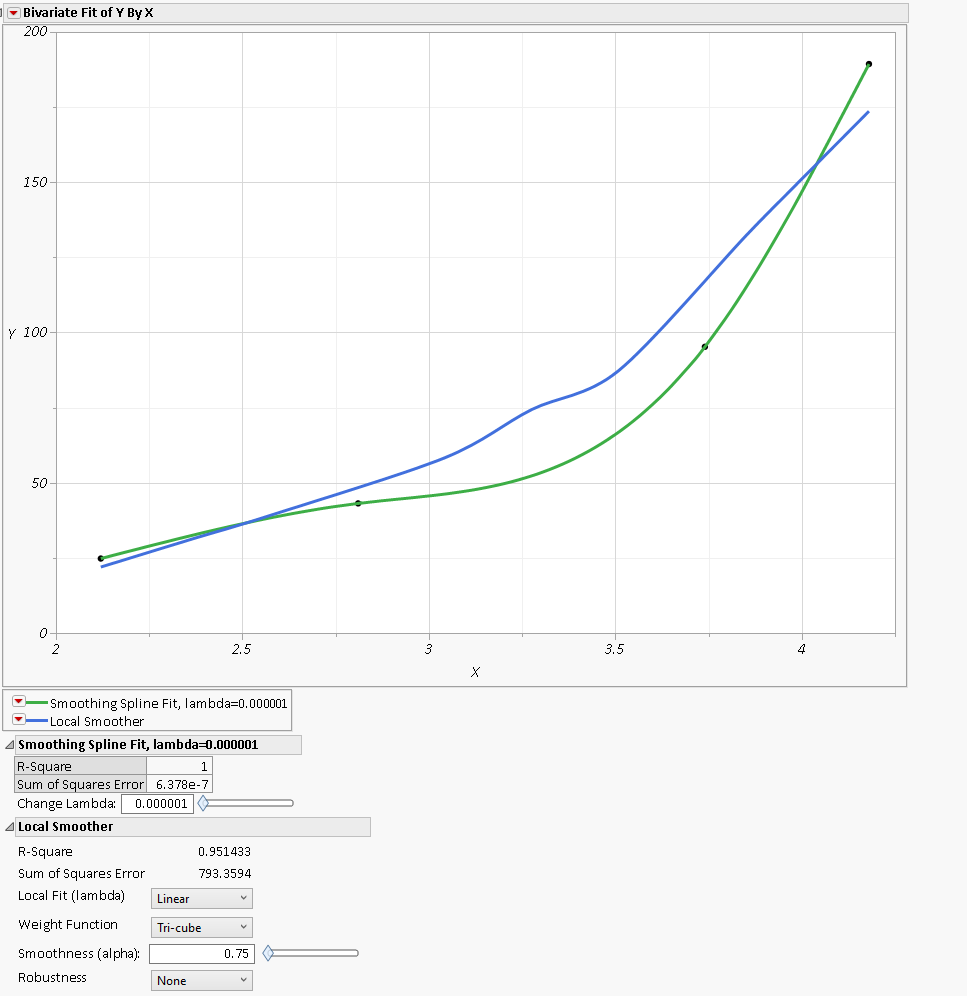
In JMP, I did Fit Y by X
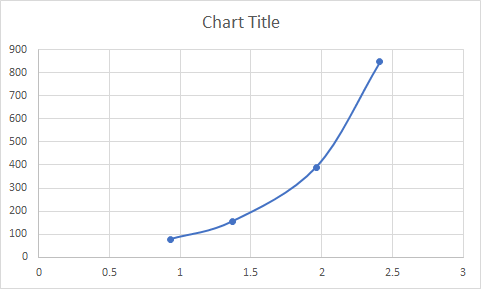
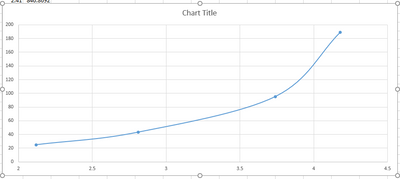
If I input the same data in Excel
I get this
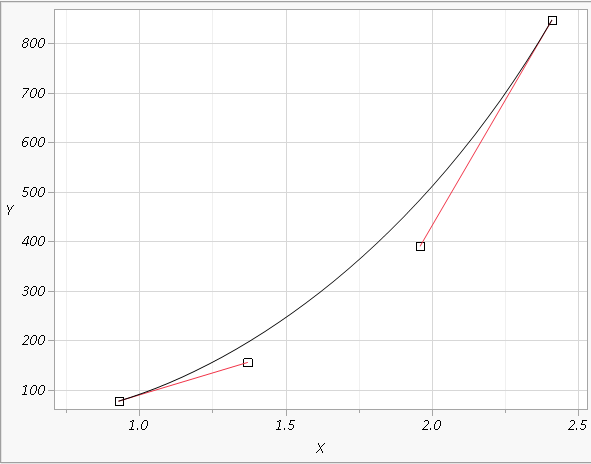
Notice in JMP green line there a bit of an oscillation/ kink in the curve around lower left (between X values 2-3), whereas in Excel that is not the case.
my end goal is to interpolate values from the line, so if Excel and JMP gives two different lines, then I would end up with different interpolation values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
The spline chooses a slope at the beginning and end that does not appear to be the same for JMP and Excel. The spline uses a different cubic between each pair of points and can smoothly join a large number of points, matching slopes and curvatures. If you only have four points, it might make sense to fit a cubic to the four points and use the formula to do the interpolation.
Maybe we'll get a statistician's answer.
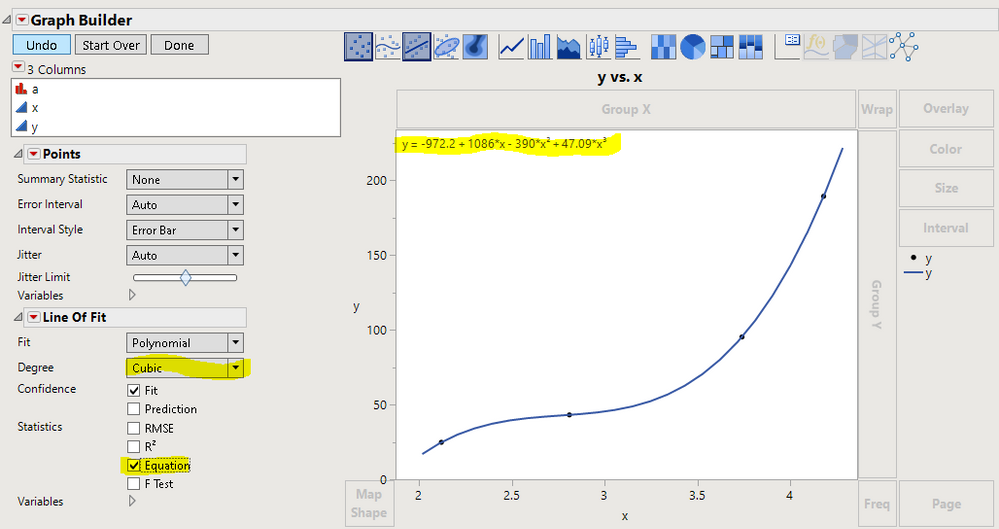
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
Yes. I hoping for that.
Another way to do this -- > maybe we can calculate the control point based on the four known points I have on the curve and then draw bezier curve passing through all four points. is there a way to do that?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us