- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Where I work, we generally perform DOEs to verify that a machine is capable before we release it to manufacture saleable product.
Generally the DOE studies require that we meet a certain Cpk or Sigma-quality level for each run. So I analyze the resulting data by fitting a curve, and JMP outputs a Cpk and predicted PPM defective. I use the Cpk to justify that the study results are acceptable.
I have a couple of questions that have been bothering me for too long:
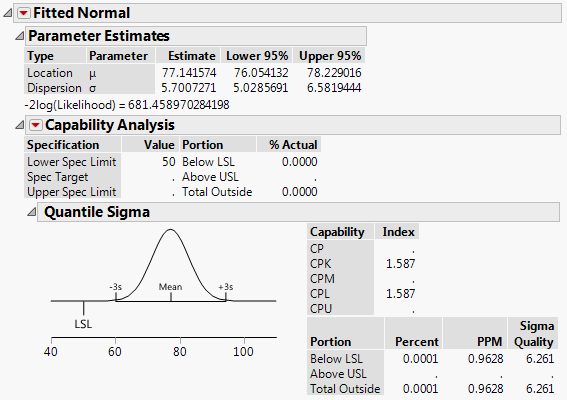
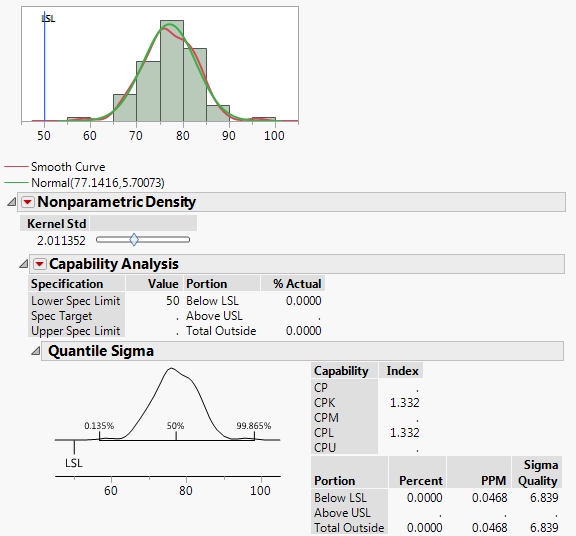
1a. I've often found that where JMP reports a Cpk, the PPM it predicts does not match with sources I find online (i.e Cpk=1.33 and ppms are 6210 online vs. ~0.05 in JMP).
Why? It's not even close.
See the attachments for examples I'm referring to. One fits a smooth curve. The other fits a non-parametric curve to the same data.
1b. Why does the normal distribution, with the higher Cpk, also have a higher PPM?
2. In review of the same study report, I was asked "Why is a Cpk of 1.33 right for this process?"
Normally I would say "Well a Cpk of X is correlated to ppm defective of XXX PPM," or something along those lines. However finding the inconsistency related to question 1 above threw a wrench into this idea - so I came here.
How would you recommend justifying a Cpk?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Peter,
I'm right with you on the issue of using "Cpk" as a metric from this type of experiment.
Just to make sure I'm on the same page with all of you. We're running an experiment where each experimental unit generate sa series of parts that are all measured. I'm assuming that in this experiment the parts are measured sequentially, rather than dumping all the parts in a bin and measuring in a more or less random sequence.
This is a repeated measures problem with, at the very least, a AR-1 covariance structure.
Cpk is super dangerous in this situation because the Sigma is an estimate of the standard deviation based on the moving range. When the process (which is the experimental unit in this case) is stable and in control the "Within Sigma" for Cpk is approximately equal to the "Overall Sigma / Standard Deviation). However, if the process has start up noise or drift, the Within Sigma is oblivious to this Overall variation, and we will end up with a blissfully uninformed view of the process generated by this exprimental unit of the DOE. Another way to say this, is that if the parts generated by the process exhibit autocorrelation (the measurement of the current part is a good predictor of the next part, due to drift in one direction) then the Within Sigma is likely to be much smaller than the Overall Sigma and the parts from this run of the expeiment will look fantastic from a Cpk perspective (and even better if the average happens to be close to the target.)
Parameters can be good responses in a DOE, and Mixed Models aren't always necesary. Things like Mean, Standard Deviation, or Duration of start up noise, slope of drift (parameterization of the time series data). However, parameters that mask what we are trying to measure and not very helpful. As it turns out, JMP has a really powerful tool for optimizing a DOE model to find the region of the design space with the lowest defect rate. John Sall presented this feature and a use case in his talk at Discovery 2017.
https://community.jmp.com/t5/Discovery-Summit-2017/2017-Plenary-John-Sall-Ghost-Data/ta-p/46090
go to this time index 43:20
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us