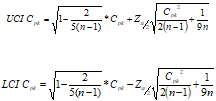- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Where I work, we generally perform DOEs to verify that a machine is capable before we release it to manufacture saleable product.
Generally the DOE studies require that we meet a certain Cpk or Sigma-quality level for each run. So I analyze the resulting data by fitting a curve, and JMP outputs a Cpk and predicted PPM defective. I use the Cpk to justify that the study results are acceptable.
I have a couple of questions that have been bothering me for too long:
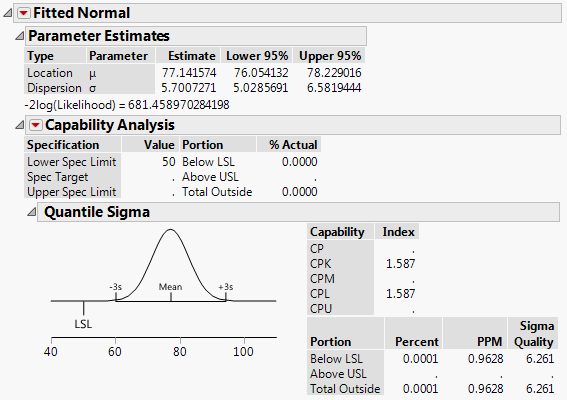
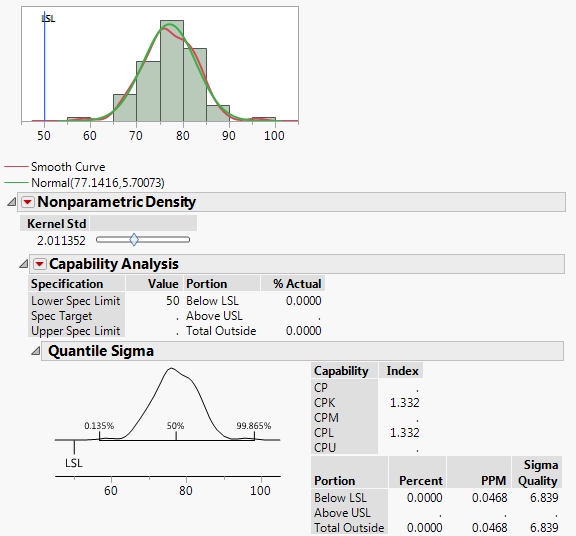
1a. I've often found that where JMP reports a Cpk, the PPM it predicts does not match with sources I find online (i.e Cpk=1.33 and ppms are 6210 online vs. ~0.05 in JMP).
Why? It's not even close.
See the attachments for examples I'm referring to. One fits a smooth curve. The other fits a non-parametric curve to the same data.
1b. Why does the normal distribution, with the higher Cpk, also have a higher PPM?
2. In review of the same study report, I was asked "Why is a Cpk of 1.33 right for this process?"
Normally I would say "Well a Cpk of X is correlated to ppm defective of XXX PPM," or something along those lines. However finding the inconsistency related to question 1 above threw a wrench into this idea - so I came here.
How would you recommend justifying a Cpk?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Hi, Matt2!
Many statisticians dislike Cpk and Process Capability Indicators intensely, for many reasons:
- Prone to poor/naïve interpretations.
- Fundamental assumptions are often violently violated.
- Evil manipulations of these indicators are prevalent among some quality practitioners.
- Too often reported as point estimates with no regard to their sampling error.
- Over-simplify process characteristics.
Many references (Montgomery, Wheeler, Kotz & Lovelace) document the “misuses”, “fantasy…and outright delusions”, and “statistical terrorism” of Cpk and Process Capability Indicators.
I find it very difficult to justify any Cpk, especially with small sample sizes. My experience suggests that one needs larger sample sizes than one can realistically get from DOE's...considerably greater than 200...sometimes much larger than 5000, depending on the calculation method.
All that said, looking at your data is better than not looking. Cpk is better than nothing, as long as you're pragmatic about it and use that power for good and not evil. You may wish to try Cpk confidence intervals (I and others like the Nagata & Nagahata 1999), and use the LCI as an arbiter of manufacturability.
Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Hi, Matt2!
Many statisticians dislike Cpk and Process Capability Indicators intensely, for many reasons:
- Prone to poor/naïve interpretations.
- Fundamental assumptions are often violently violated.
- Evil manipulations of these indicators are prevalent among some quality practitioners.
- Too often reported as point estimates with no regard to their sampling error.
- Over-simplify process characteristics.
Many references (Montgomery, Wheeler, Kotz & Lovelace) document the “misuses”, “fantasy…and outright delusions”, and “statistical terrorism” of Cpk and Process Capability Indicators.
I find it very difficult to justify any Cpk, especially with small sample sizes. My experience suggests that one needs larger sample sizes than one can realistically get from DOE's...considerably greater than 200...sometimes much larger than 5000, depending on the calculation method.
All that said, looking at your data is better than not looking. Cpk is better than nothing, as long as you're pragmatic about it and use that power for good and not evil. You may wish to try Cpk confidence intervals (I and others like the Nagata & Nagahata 1999), and use the LCI as an arbiter of manufacturability.
Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
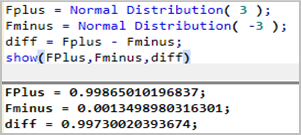
The relationship between process capability and ppm defective is, I think, easier to explain by using Cp. In particular, for Cp=1 the (two-sided) spec limits hae a width of 6 sigma. For a normal distribution 99.73% of the data is contained within the 6 sigma width. With some simple JSL you can do the calculation yourself:
Therefore 0.27% is outside of spec; equivalent to 2,700 ppm.
You can do similar calculations for Cpk values.
These calculations are based on probabilities from a Normal distribution. Whilst the calculations can be generalised to other distribution types the figures you find online will almost certainly be based on a Normal distribution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Hi, Matt2!
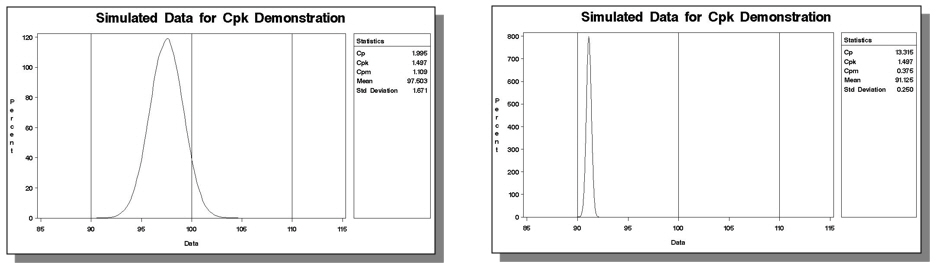
And David alludes to an important point: If one cares about their process being on target (and one should!), one should specify both Cpk and Cp.
If a process is perfectly centered, Cp = Cpk. Motorola used to define Six Sigma as a Cp > 2.0 and a Cpk > 1.5, for instance.
A process can operate with a high Cpk and be operating very, very far from target. Both these simulated processes have a Cpk of 1.5:
Of course, Cp isn't easily defined for a one-sided spec limit like your example.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Thanks for everyone's replies. Very good information. I'd like to build on it with some follow-up questions.
I will keep Cp in mind for later studies with 2-sided specs.
I found that the product's lot release spec lists an AQL and a minimum Ppk. In the abscence of a caculated Cp, would it be justifiable to target a defect rate for a qualification study of say AQL/2 or the Ppk+0.5?
Kevin, I found only a publication from Nagata and Nagahata from 1994. If there is one for 1999, can you provide it?
I'm still not sure why the Cpk and ppm values don't correlate exactly to one another. Are they not derived by the same path in JMP?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Hi, Matt2!
Kotz and Lovelace reference Nagata and Nagahata 1994, so that's the right one.
The formulae in K&L are
Here's a JSL function that might prove useful, even though it is misnamed :) :
N2CpkCI1999 = Function({Cpk,n,alpha},{Default Local},
LCI=Root(1-2/(5*(n-1)),2)*Cpk-Normal Quantile(1-alpha/2)*Root(Cpk^2/(2*(n-1))+1/(9*n),2);
UCI=Root(1-2/(5*(n-1)),2)*Cpk+Normal Quantile(1-alpha/2)*Root(Cpk^2/(2*(n-1))+1/(9*n),2);
EvalList({LCI,UCI})
);
{UCI, LCI} = N2CpkCI1999(1.5, 30, 0.05);
/* Log prints {1.08557750374946, 1.89366100113153}Note that a Cpk of 1.5 with 30 samples yields a LCI of 1.09...from "capable" to "barely capable".
I believe the nonparametric Cpk is calculated using the percentile method. That method is almost always biased high (sometimes ridiculously so), and requires huge sample sizes to be accurate...that's the one that requires n >= 5000 in my experience.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
It seems nobody answered the part about why the Cpk's and ppm's do not "correlate".
In the traditional SixSigma calculation, a 1.5 sigma shift is assumed to account for process shift or batch/batch variation. This means that at 6sd (standar deviations), you need to subtract 1.5sd. If you look at the tail of a normal distribution, you will find the 3,4 dppm. In JMP you can write:
(1-Normal Distribution(4.5))*1e6At at Cpk of 2, JMP simply reports the tail at 6sd's:
(1-Normal Distribution(6))*1e6So to translate from JMP dppm to SixSigma dppm, simply subtract 1,5sd's
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Matt:
Can I ask a few questions? Your second paragraph in your original post raises some questions in my mind. Copy/pasted here:
"Generally the DOE studies require that we meet a certain Cpk or Sigma-quality level for each run. So I analyze the resulting data by fitting a curve, and JMP outputs a Cpk and predicted PPM defective. I use the Cpk to justify that the study results are acceptable."
Can you describe why you feel a specific run in a designed experiment needs to 'meet a certain Cpk..for each run'? The notion a calculating a Cpk for reponse results from a DOE doesn't make sense to me. Generally speaking, process capability indices have as an assumption constant mean and variance across the population of observations included in the calculation of the indices. In a designed experiment our usual intent is to have a NON constant mean for responses (the signal we're looking for), and in some select types of experimental investigations, non constant variances as well (when a variance signal is what we're after) This is the whole idea of DOE providing a means by which we can see a signal rise above the noise.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
Hi, Peter!
We can certainly discuss a) if these are DOE's, and b) if there's enough "fantasy...and outright delusion" to go around, but it was fairly common in the semiconductor industry to run process window experiments, varying process inputs around allowable ranges, and then assessing if the process output was capable. As I mentioned above, the samples sizes from these "DOE's" are usually woefully inadequate for any useful information, but they still had to be run, usually by fiat.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do Cpk and Sigma relate to ppm defective, and how do I justify a Cpk?
@Kevin_Anderson No need to discuss...I understand completely your last concept. Back in my day at Kodak as a statistician working on inumerable new product commercialization programs, where DOE was the centerpiece of our product/process design work...we did exactly as you describe as well. I have no quarrel or objection to using simulation within say, the JMP Prediction Profiler, to create estimated process capability indices in this manner.
As you mention...we can discuss the merits of the simulation assumptions 'till we're blue in the face...as well as the often times arbitrary assignment of 'magic' process capability targets like 1.0, 1.33 or the chimeric Cpk = 1.5 for the magical "Six Sigma" goal. That's a philosophical discussion over several adult beverages some day if we ever cross paths :)
The issue I was asking the OP was he didn't explicitly say this is what he's doing. Maybe I'm just being too 'literal man' here. Again I go back to trying to ascribe a Cpk to a population of responses from within a designed experiment is a gross misapplication of both DOE and process capability analysis. And if I read what he wrote...that's what it sure sounds like he might be doing? I sure hope not...but I felt compelled to ask.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us