- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How are the p-values calculated from the S test statistic in the Wilcoxon signed...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How are the p-values calculated from the S test statistic in the Wilcoxon signed rank test in JMP?
Hi, I'm trying to make sure I understand how the S test-statistic and corresponding p-values are being calculated in the Wilcoxon Signed Rank test in JMPs Matched Pairs Platform. For example, if I compare two columns of data using the Matched pairs analysis in JMP and selected the Wilcoxon Signed Rank option, I see a Test Statistic S= 15.5 and a Prob>|S|= 0.2832. I'm wondering what distribution of S (or other strategy) is JMP is using to calculate the p-value?
I can see from the basic analysis JMP pdf that W is computed as equal to 1/2 (sum of signed ranks). I'm assuming that W is equivalent to S in this case. Is that correct?
And again, I'm not sure how the p-value is calculated here.
I'm confused as to how the JMP output compares to, for example, calculating a test-statistic and determining whether it is a less than a given value (as a function of the sample size) in order to determine whether to reject the null hypothesis that the medians are the same.
Thank you in advance for any help! I really appreciate it!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How are the p-values calculated from the S test statistic in the Wilcoxon signed rank test in JMP?
You're correct--W is the same as S. If # of pairs, n, is less or equal to 20, the p-value is computed from the exact distribution of W, where the distribution is a convolution of scaled binomial distributions. When n >20, the p-value is computed using a Student’s t approximation. Check out statistical details by scrolling down to Wilcoxon Signed-Rank Test Statistic on this page Statistical Details for the Distribution Platform
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How are the p-values calculated from the S test statistic in the Wilcoxon signed rank test in JMP?
Correct—the mean of a binomial random variable is n*p.
The W statistic you referred to, as shown in JMP documentation, is 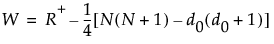
W is expected to be zero under the null hypothesis H0: median of a single population of paired differences is 0, assuming that the underlying population is symmetric. So, either a larger or a smaller than the expected R+ leads to a larger abs(W).
Back to your question, having a larger R+ doesn’t necessarily mean a smaller d0 since R+ is the sum of the ranks for positive-signed pairs, and d0 depends not only on N+, but also N-.
Mean of a binomial distribution represents the # of times W is expected to be zero under H0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How are the p-values calculated from the S test statistic in the Wilcoxon signed rank test in JMP?
You're correct--W is the same as S. If # of pairs, n, is less or equal to 20, the p-value is computed from the exact distribution of W, where the distribution is a convolution of scaled binomial distributions. When n >20, the p-value is computed using a Student’s t approximation. Check out statistical details by scrolling down to Wilcoxon Signed-Rank Test Statistic on this page Statistical Details for the Distribution Platform
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How are the p-values calculated from the S test statistic in the Wilcoxon signed rank test in JMP?
Thank you for your help jiancao!
So, is it correct to say that the mean of the binomial distribution is a function of the number of matched pairs that I am comparing?
And if the null hypothesis is that the difference between the medians of the matched pairs is zero, then I'm confused about the relationship between the test statistic W and the p-value. From the Statistical Details, I would expect that W will be bigger as the differences between the medians become bigger because there are fewer pairs where the difference between the pairs is zero. So I would expect d0 to be small and R+ to be larger. So I would expect that as R+ gets larger and W gets larger (depending on N), that the p-value would become smaller because W is becoming larger (and thus farther from the mean of the binomial distribution?), Is this correct? Also, does the mean of the binomial distribution represent the mean of the probabilities that the medians of the matched pairs are not different? Again-thank you very much for your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How are the p-values calculated from the S test statistic in the Wilcoxon signed rank test in JMP?
Correct—the mean of a binomial random variable is n*p.
The W statistic you referred to, as shown in JMP documentation, is 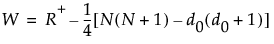
W is expected to be zero under the null hypothesis H0: median of a single population of paired differences is 0, assuming that the underlying population is symmetric. So, either a larger or a smaller than the expected R+ leads to a larger abs(W).
Back to your question, having a larger R+ doesn’t necessarily mean a smaller d0 since R+ is the sum of the ranks for positive-signed pairs, and d0 depends not only on N+, but also N-.
Mean of a binomial distribution represents the # of times W is expected to be zero under H0.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us
